Hirdetés
Talpon vagyunk, köszönjük a sok biztatást! Ha segíteni szeretnél, boldogan ajánljuk Előfizetéseinket!
Új hozzászólás Aktív témák
-

VoidXs
nagyúr
Mielőtt megmutatom a megoldást, szeretném hangsúlyozni, hogy ezek a feladatok soha nem gyakorlatiak, a brute force (rajzolgatás, hátha kijön) sosem ér maximum pontot, csak indirekt bizonyítási esetekben.
Ha N darab egyenesed van, amik definíció szerint végtelen hosszúak, és egyik se párhuzamos semelyik másikkal, minden esetben minden egyenesen N - 1 metszéspontod lesz. Ez azért van így, mert valahol bármelyik kettő garantáltan metszeni fogja egymást, hiszen nem párhuzamosak. 4 esetén mind a 3 másikkal lesz egy metszésed. Mivel egy egyenesen N - 1 metszés van, ezért a majdnem végleges megoldás N * (N - 1), de ezt meg kell felezni, hiszen mindkét metsző egyenes szemszögéből leszámoltuk.
A végső megoldás tehát azt mondja, hogy N darab, páronként nem párhuzamos egyenes esetén pontosan N * (N - 1) / 2 metszéspont lesz, ami 4 egyenesnél 4 * 3 / 2 = 6 metszés. 5 nem fordulhat elő, az azt jelenti, hogy csak nem húztad elég hosszan az egyeneseket. Ha elég hosszan húzod, bárhogyan rajzolod fel őket, fixen 6 lesz:
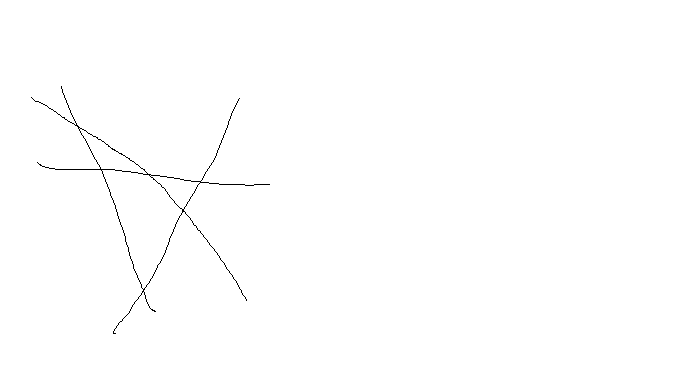
És ez az, ami miatt a rajzolás nem elégséges válasz, mert szinte mindig ki fog jönni próbálgatással, csak azt nem tudjuk, hogy miért.
-
-

axioma
Topikgazda
Itt nem tudok jol rajzolni, de nem jol erted.
A haromszog: origo (ha jol ertem onnan indulsz), a fordulasi pont (ertsd: addig csak az egyikfajta iranyu vektorokat hasznalod), es a vegpont, ahova mesz a fordulastol csak a masikfajta vektorokkal.
Geogebrabol sikerult: [kép]
Nem egeszen ara'nyos, de a ket baloldali vektor helyett lesznek a sok kicsibol osszeadottak, a jobb oldali az eredmenyvektor. A koztes pontot, pontosabban annak tavolsagat az origotol es a celponttol kell tudni, es utana lehet mar ladapakolni. -

axioma
Topikgazda
TDX kb. osszefoglalta, a gyakorlatban neked tulkepp csak az kell, hogy milyen osszes hossz kell legyen az egyik es masik fajtabol. Az meg lehet nagyon konnyu meg nagyon nehez is. Ha ez me'g mindig a terkepes feladat es van egy tures a dologban, akkor siman ladapakolasi algoritmussal tudsz nagy valoszinuseggel mohoval is jot talalni (becslesnek azt mondanam, varhatoan a legkisebb hossznal kisebb hibat ki kellhet tudni hozni). Ha tuti az optimalis kell (azaz aminel nincs elvileg sem jobb), az meg akar lehet NP-teljes (ld. tavaly osszel a prog.topikban egy forumozo amokfutasat a rudak vagdosasa kapcsan, de a lenyeg az megvolt matekilag).
-

TDX
tag
Ha két fajta irányba mutató vektorokból szeretnél egy harmadik irányba mutatót csinálni, akkor szerintem azt a következőképp a legegyszerűbb kiszámolni.
Mivel a vektorok összeadása kommutatív (tehát a+b az ugyanaz mint b+a, vagyis a sorrend nem számít), ezért felteheted, hogy az első irányba adod először össze a vektorokat (amiket használsz abban az irányban), majd a másik irányba amiket abba az irányba használsz.
Így egy háromszög két oldalát járod be, amiknek tudod az irányait (hiszen azok megegyeznek az egyes vektorok irányaival). Sőt, a harmadik oldalnak is tudod az irányát, hiszen az lesz az az irány, amerre az eredményvektor mutatni fog.
Ebből könnyen ki tudod számolni a háromszög szögeit. Jelen esetben 40°, 110°és 30°-ot fogsz kapni a háromszög szögeire. 30° azzal az oldallal szemben, ami 10°-ot zár be az x tengellyel, 40° azzal az oldallal szemben, ami 80°-ot zár be vele.
Ebből a szinusz-tétel megmondja, hogy azon oldalak hosszainak aránya az sin(30°)/sin(40°). Ezt ki tudod számolni számológéppel hogy pontosan mennyi.
Innen már csak választanod kell a két irányba mutató vektorok közül 1-1 részhalmazt, amiknek a hosszösszegeinek aránya pont sin(30°)/sin(40°) lesz. Nem tudom hogy erre van-e jó módszer, kézzel kell-e megtalálnod, esetleg programot írnod rá, de ha kézzel kell megkeresned, gondolom nincs sok vektor és nem lehet túl nehéz. Ha programot kéne írni rá, akkor valaki nálam programozásból okosabb biztos tud segíteni. -

axioma
Topikgazda
Varj, en nem sugarat mondtam. Metszd el az egeszet, es szamold meg, hany metszespont van azok kozul a pont felett. Ehhez kell:
0. elek tarolasa ugy, hogy (x1,y1,x2,y2) alakban x1<=x2
1. e'l ellenorzese hogy az x=P[0] metszi-e (x1<P[0]<x2, egyenloseg ugyis kulon kezelendo)
2. a skalarszorzatos modszerrel megallapitod, hogy P jobbra van-e az igy allo szakasztol (ha igen, az e'l felette metszi)
3. hany felette metszo van
Az xy teglalap nem teljesen vilagos, de ugy ertettem, hogy a P benne van az el altal meghatarozott teglalapban, az biztosan nem elegendo vizsgalatra (pl. egyszeru stopp-tabla es a kozepso pont, egy ilyen elet se fogsz talalni). -

axioma
Topikgazda
Azt konnyu megallapitani, h melyik elet metszed [ha az e'let nemcsokkeno x szerint ta'rolod, koztuk legyen a P-e']. Ezutan mar csak az a kerdes, 'alatta' van-e a P pont az egyenese'nek, arra meg akkor bevetheted @kovisoft modszeret. Ezeket nekem konnyunek tunik osszeszamolni.
Nyilvan a fuggoleges e'lek igenyelnek egy kis plusz if-elgetes.
Ha programot irsz mert sokszor kell ugyanarra a poligonra mas-mas P-kre valaszolni, es nem eri el a sokezres nagysagrendet a poligon csucsainak szama, akkor az erintett csucsok kivalasztasahoz csinalhatsz elofeldolgozast: adott x letezo erteknel mely indexuek kisebb bal vegpontuak, illetve masik tombben x-nel mely indexuek nagyobbak, akkor egy halmazmetszet a vizsgalando indexek listaja. -

TDX
tag
A fentebb írt válaszok mellett könnyű kihozni egy megoldást baricentrikus koordinátákkal. A baricentrikus koordinátázás annyi dióhéjban, hogy ha veszel egy X pontot a síkon kívül, és van ABC három nem egy egyenesre eső pontod a síkon, a vektor az X-ből A-ba mutató vektor és hasonlóan b, c, akkor a sík azon pontok halmaza, amikhez αa+βb+γc vektor mutat X-ből, ahol α+β+γ=1.
Ez komplikáltnak tűnhet, de ebben a rendszerben az ABC háromszög pontjai pontosan azok lesznek, amikre α, β és γ is nemnegatív. Belső pontok pedig azok, melyekre mindhárom szigorúan pozitív.
Ezt pedig a következőképp lehet alkalmazni annak a kiszámolására, hogy belső pontról van-e szó. Az X-szel nem törődünk itt, hanem csak a síkban dolgozunk, legyenek a három csúcs koordinátái (x1,y1), (x2,y2), (x3,y3), és legyen P-é (x,y). Ekkor keressük a fentebbi α,β,γ-t.
Behelyettesítve gammára, és keveset számolva kijön a következő egyenlet (sajnos nem tudom, hogy hogy lehet könnyen mátrixokat leírni itt):
(x1-x3 x2-x3) (α) (x-x3)
(y1-y3 y2-y3) (β) = (y-y3)Ezt alfa és bétára megoldva ha olyan értékek jönnek ki, hogy mind alfa, mind béta és mind (1-α-β) nemnegatív, akkor P pont rajta van a háromszögön, és ha mindhárom érték pozitív, a belsejében van.
-

kovisoft
őstag
Azt kell megnézni, hogy a háromszög oldalait körbejárva a p1 pont mindig ugyanúgy balkéz vagy mindig ugyanúgy jobbkéz felé esik-e. Ha igen, akkor a pont a háromszög belsejében van.
Ehhez venni kell sorban a háromszög oldalvektorainak (A->B, B->C és C->A) a normálvektorát, amit mindhárom esetben ugyanúgy kell meghatározni (pl. mindig balra 90 fokot forgatva, azaz felcseréljük a koordinátáit és mondjuk mindig az x-nek az előjelét változtatjuk meg). Meg kell nézni az oldalszakasz kezdőpontjából a p1 pontba mutató vektor és a normálvektor skaláris szorzatának az előjelét. Ha az mindhárom esetben ugyanolyan előjelű, akkor a pont a háromszög belsejében van.
-
-

kovisoft
őstag
Mindkét normálvektorról külön-külön el tudod dönteni, hogy a másik háromszög felé mutat-e vagy ellenkező irányba. Mégpedig úgy, hogy kiszámolod az adott háromszög normálvektorának és egy ebből a háromszögből a másik háromszögbe mutató vektornak (pl. a másik háromszög 3. csúcsába mutató vektornak) a skaláris szorzatát. Ha ez a szorzat pozitív, akkor a normálvektor a másik háromszög felé mutat.
-

kovisoft
őstag
Nézzük meg, mit is jelent az F(5)=12:
Modulo p=5 a szóba jöhető 1<=a, b, c<p értékek az 1, 2, 3, 4 lehetnek. Ezek harmadik hatványai (szintén modulo 5): 1^3=1, 2^3=3, 3^3=2, 4^3=4. Ezekből 12-féleképpen lehet előállítani az a^3+b^3=c^3 (mod 5)-öt: 1+1=2, 1+2=2+1=3, 1+3=3+1=4, 2+2=4, 2+4=4+2=1, 3+3=1, 3+4=4+3=2, 4+4=3.
Új hozzászólás Aktív témák
- Azonnali fotós kérdések órája
- AMD Navi Radeon™ RX 9xxx sorozat
- Három Redmi 15 érkezett a lengyel piacra
- Túra és kirándulás topic
- gban: Ingyen kellene, de tegnapra
- Subaru topik
- Lexus, Toyota topik
- Hitelkártyák használata, hitelkártya visszatérítés
- Apple MacBook
- Épített vízhűtés (nem kompakt) topic
- További aktív témák...
- GYÖNYÖRŰ iPhone 11 64GB Purple -1 ÉV GARANCIA - Kártyafüggetlen, MS2190, 100% Akkumulátor
- HIBÁTLAN iPhone XS Max 64GB Gold -1 ÉV GARANCIA - Kártyafüggetlen, MS2898, 100% Akkumulátor
- HP 200W (19.5V 10.3A) kis kék, kerek, 4.5x3.0mm töltők + tápkábel, 928429-002
- REFURBISHED és ÚJ - HP USB-C/A Universal Dock G2 docking station (5TW13AA) (DisplayLink)
- Tablet felvásárlás!! Apple iPad, iPad Mini, iPad Air, iPad Pro
Állásajánlatok
Cég: FOTC
Város: Budapest


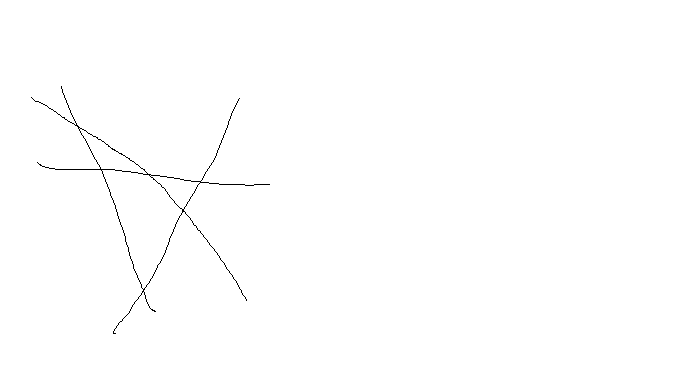








 , van a városi könyvtárban is egy (elvileg).
, van a városi könyvtárban is egy (elvileg). axioma
axioma
