- Samsung Galaxy Watch6 Classic - tekerd!
- Milyen okostelefont vegyek?
- Samsung Galaxy S23 és S23+ - ami belül van, az számít igazán
- Samsung Galaxy Watch7 - kötelező kör
- Tíznaponta azért tedd töltőre az Ulefone-t!
- Hivatalosan is bemutatta a Google a Pixel 6a-t
- Kezünkben a Honor Magic V5
- Újabb magyar banknál elérhető a Xiaomi Pay
- Samsung Galaxy S24 Ultra - ha működik, ne változtass!
- A lapkakészlet és az akku különbözteti meg a Motorola Edge 60 és Edge 60 Pro-t
Hirdetés
Talpon vagyunk, köszönjük a sok biztatást! Ha segíteni szeretnél, boldogan ajánljuk Előfizetéseinket!
Új hozzászólás Aktív témák
-
VoidXs
nagyúr
Wow, ez a komment de rég volt. A választ 3 éve keresem, végre megtaláltam, és ordenáré hülyének érzem magam, hogy ezt egy jó Google keresés megtalálta volna... A DCT 4. verzióját írtam le, csak a dokumentum, ahonnan szedtem a képletet, ezt elfelejtette közölni, csak az algoritmust írta le...
-
VoidXs
nagyúr
Mielőtt megmutatom a megoldást, szeretném hangsúlyozni, hogy ezek a feladatok soha nem gyakorlatiak, a brute force (rajzolgatás, hátha kijön) sosem ér maximum pontot, csak indirekt bizonyítási esetekben.
Ha N darab egyenesed van, amik definíció szerint végtelen hosszúak, és egyik se párhuzamos semelyik másikkal, minden esetben minden egyenesen N - 1 metszéspontod lesz. Ez azért van így, mert valahol bármelyik kettő garantáltan metszeni fogja egymást, hiszen nem párhuzamosak. 4 esetén mind a 3 másikkal lesz egy metszésed. Mivel egy egyenesen N - 1 metszés van, ezért a majdnem végleges megoldás N * (N - 1), de ezt meg kell felezni, hiszen mindkét metsző egyenes szemszögéből leszámoltuk.
A végső megoldás tehát azt mondja, hogy N darab, páronként nem párhuzamos egyenes esetén pontosan N * (N - 1) / 2 metszéspont lesz, ami 4 egyenesnél 4 * 3 / 2 = 6 metszés. 5 nem fordulhat elő, az azt jelenti, hogy csak nem húztad elég hosszan az egyeneseket. Ha elég hosszan húzod, bárhogyan rajzolod fel őket, fixen 6 lesz:
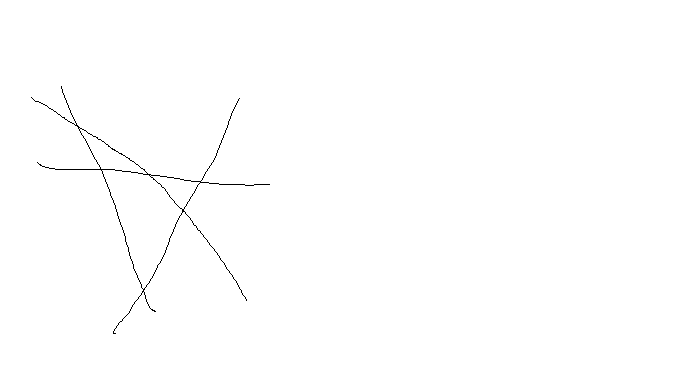
És ez az, ami miatt a rajzolás nem elégséges válasz, mert szinte mindig ki fog jönni próbálgatással, csak azt nem tudjuk, hogy miért.
-
#6660
VoidXs
nagyúr
hiperFizikus
#6659
VoidXs
nagyúr
válasz
hiperFizikus
#6659
üzenetére
Prímszámokról beszélünk, tehát triviális, hogy 0 megoldásuk lesz:
- Szorzás: két szorzat akkor egyenlő, ha a prímtényezős felbontásuk azonos. Ha mindkét oldal más prímekből áll, nem lehet azonos.
- Osztás: a/b=b/c esetben azt kellene bizonyítanod, hogy b=n*a és c=n*b, vagyis nem lennének prímek.
- Hatvány: mint a szorzásnál, prímtényezős felbontásokat készítesz, amik a kitételeid miatt soha nem lehetnek egyenlők. -
#6658
VoidXs
nagyúr
hiperFizikus
#6657
VoidXs
nagyúr
válasz
hiperFizikus
#6657
üzenetére
Ez meg megint a Goldbach-sejtés. Ha megoldod, rögtön hozzád fognak vágni 1 millió dollárt, viccen kívül.
-
#6656
VoidXs
nagyúr
hiperFizikus
#6654
VoidXs
nagyúr
válasz
hiperFizikus
#6654
üzenetére
Nem tudsz vele tovább jutni:
- ha x 3-as maradéka 0, akkor x osztható 3-mal,
- ha x 3-as maradéka 1, akkor x+2 osztható 3-mal,
- ha x 3-as maradéka 2, akkor x+4 osztható 3-mal.#6655 egyenletrendszere pedig, ha jól értem: a + b = b + c, és a, b, c prímek. Ekkor csak egy megoldás létezhet, a triviális, hiszen ha b kiesik, akkor a = c marad, és b a kiesés által szabad változóvá válik. Ha kikötöd, hogy a < b < c, akkor a megoldás üres halmaz, hiszen ha a = c, akkor b nem lehet az egyiknél kisebb, a másiknál pedig nagyobb.
-
#6653
VoidXs
nagyúr
hiperFizikus
#6652
VoidXs
nagyúr
válasz
hiperFizikus
#6652
üzenetére
2-vel csak a 3, 5, 7 működik, nincs más, a fent említett okokból.
-
-
#6646
VoidXs
nagyúr
hiperFizikus
#6645
VoidXs
nagyúr
válasz
hiperFizikus
#6645
üzenetére
Magyarul olyan a - b = b - c esetet keresel, ahol a, b, c prím, erre rengeteg példa van a tiéden kívül, pl. 3 - 7 = 7 - 11, vagy 5 - 11 = 11 - 17. Valószínűsíthető, hogy végtelen ilyen számhármas létezik, de jelenleg a matematika egy meg nem oldott problémája, hogy milyen szabályrendszer van prímek távolsága közt (a Goldbach-sejtést kellene hozzá megoldani). Programmal könnyen találsz rengeteg ilyet, de egy idő után már nagyon lassan dobál ki új számokat.
-
#6626
VoidXs
nagyúr
hiperFizikus
#6625
VoidXs
nagyúr
válasz
hiperFizikus
#6625
üzenetére
Ha már rögtönzött filozófia topikot tartunk senki élvezetére, olvasd el inkább újra, emészd egy kicsit.
-
#6624
VoidXs
nagyúr
hiperFizikus
#6623
VoidXs
nagyúr
válasz
hiperFizikus
#6623
üzenetére
Nem vagyok matematikus, de egy értelmiségi előtt két út van, az egyik az alkoholizmus, a másik járhatatlan. Szóval általában szarul.
-
#6622
VoidXs
nagyúr
hiperFizikus
#6621
VoidXs
nagyúr
válasz
hiperFizikus
#6621
üzenetére
Mire jutok mivel?
-
#6620
VoidXs
nagyúr
hiperFizikus
#6619
VoidXs
nagyúr
válasz
hiperFizikus
#6619
üzenetére
Embeddált bizonyítás nélkül nem értem, hogy mi itt a nagy újdonság. Ha itt arra gondolnak, hogy C = 90° esetén a szinusztételből
a = c * sin(A),
és
b = c * sin(B) = c * cos(A),
mert A + B = 90°, akkor behelyettesíted Pitagoraszba, és kijön, hogy c^2 = c^2. Ezt tényleg össze lehet rakni középiskolában, max azt tudom elképzelni, hogy igény hiányában nem írta le senki, bár az is fura.Szerk: megnéztem, és persze, hogy erősen hibás volt a cikk, rengeteg előkövetelményt lehagyott, ezért nem olvasunk tech/tudomány cikkeket olyan oldalon, aminek nem ez a profilja.
-
#6617
VoidXs
nagyúr
hiperFizikus
#6616
VoidXs
nagyúr
válasz
hiperFizikus
#6616
üzenetére
Tudunk hatványozni és gyököt vonni, ennél azért jelentősen komplexebb problémaköröket szoktunk itt fejtegetni.
-
VoidXs
nagyúr
válasz
sztikac
#6598
üzenetére
Ha az ábrát negyedekre osztod, akkor átlókra vannak tükrözve, vagyis az a) terület pontosan ugyanakkora, mint a négyzet és a kör különbsége. Az a) megoldása tehát 20^2-10^2*pi. Mivel b) esetében elvettük a négyzetből a pontosan ugyanakkora külső és belső területet, a megoldás 20^2-2*(20^2-10^2*pi).
-
VoidXs
nagyúr
Biztosan nincs hozzá relatíve egyszerű zárt képlet, vagy akár szűrés a halmazra, mint például prímkeresésnél a szükséges feltételek? A végső cél egy olyan optimalizálási probléma, hogy milyen elemek esetében lehetne komplex számok amplitúdóinak gyorsabb komparáláshoz használni egy nagy halmazban az utóbbit. Mert vannak halmazok, ahol működik, csak garantálni szeretném, hogy akkor és csak akkor használom ezt a módszert, amikor garantált, hogy azonos relációkat ad.
-
VoidXs
nagyúr
Sziasztok, egy egyszerű példám lenne, amire tudom a választ, viszont brute force nélkül nem tudom bizonyítani. Hogyan lehet matematikailag belátni, hogy létezik két olyan számpár, ahol mindkettőre kiszámolva az x * x + y * y és |x| + |y| képleteket, a relációk nem lesznek azonosak?
Tehát keresem azt, hogy létezik-e olyan (x1, y1) és (x2, y2) számpár, amire:
x1 * x1 + y1 * y1 < x2 * x2 + y2 * y2 és
|x1| + |y1| > |x2| + |y2|.
Ez az állítás igaz, egy példa rá a (3, 4) és (1, 5) párok:
3 * 3 + 4 * 4 < 1 * 1 + 5 * 5 (25 < 26) és
3 + 4 > 1 + 5 (7 > 6).
Viszont hogy a megoldások halmaza mi lehet általánosan felírva, abban segítséget szeretnék kérni. -
#6439
VoidXs
nagyúr
Hegeduselekt
#6438
VoidXs
nagyúr
válasz
Hegeduselekt
#6438
üzenetére
cos x = 1/2 + cos 2x megoldása 2*(n*pi±(2±1)*pi/10, ahol n eleme Z. Ez 4 általános megoldás. Itt n=0 esetben pi/5 (36 fok) valóban egy a sok közül, de nem értem, mit akarunk belátni. Ha csak hiányzó értékeket akarunk egy táblázatból, arra ott a számológép, a jobbak szépen meg is tudják formázni.
A sin 0, 30, 45, 60, 90 és a cos ugyanezek visszafelé azért az általános iskolában tanított értékek, mert ezek eredménye sorrendben gyök(0/4), gyök(1/4), gyök(2/4), gyök(3/4), gyök(4/4), csak könnyebb őket úgy felírni, hogy 0, 1/2, gyök(2)/2 = 1/gyök(2), gyök(3)/2, illetve 1, ez viszont hiba. Nem a radián a lényeg.
Ezt a formát sok tanár csípőből benyeli tanárképzőn, és úgy adják le, hogy "ezeket meg kell tanulni és pont", mintha kiragadott random értékek lennének, pedig pont a nem egyszerűsített eredeti gyöksorozat a lényeg, hogy ha azt tudod, könnyű megjegyezni. Mivel ez egy ilyen játék, ezért köztes értékeket nem igazán érdemes keresni. Persze, lehet nagyobb osztásokat találni, gyök(n/2^x) tetszőleges x-re, de ott már nem egészek a szögek.
-
#6437
VoidXs
nagyúr
Hegeduselekt
#6436
VoidXs
nagyúr
válasz
Hegeduselekt
#6436
üzenetére
Azt valószínűleg valakinek privátban küldted véletlenül, mert a topikban csak ez a két kommented van.
-
VoidXs
nagyúr
válasz
Jester01
#6379
üzenetére
Sajnos az lenne a feladat, hogy van egy sztereo audio jel (x és y), ismert egy hang (b) keverési aránya (c1, c2), ebből kellene visszakapni a jelet az adott hang nélkül (a, c).
Viszont van egy sokkal szebb feladatom, amivel nem tudok boldogulni, és ismét segítséget kérek, remélhetőleg jó topikban.
Alapból a DFT exponense ugye i*pi/n*j*k, ahol j és k a kimeneti, illetve bemeneti elem száma. Itt a szimmetriát kihasználva könnyen tudunk FFT-t csinálni, de mi van akkor, ha nincs szimmetria, hanem i*pi/n*(j+0,5)*(k-0,5) az exponens? -
#6374
VoidXs
nagyúr
CyberPunk666
#6373
VoidXs
nagyúr
válasz
CyberPunk666
#6373
üzenetére
Köszi, tökéletesen megoldja!
-
VoidXs
nagyúr
válasz
kovisoft
#6364
üzenetére
Köszi! Sajnos szimulációval mást kaptam, kézzel a 0.18-as eredményre jutottam így:
int right = 0, total = 0;Random rnd = new Random();while (true) {double a = rnd.NextDouble() - 0.5;double b = rnd.NextDouble() - 0.5;double diff = Math.Abs(a - b);if (diff < 0.18) {if (Math.Sign(a) == Math.Sign(b))++right;++total;Console.Write($"{(double)right / total:0.0000000%}\r");}}Amit írtál, az nem csak az Y<0 eset?
-
VoidXs
nagyúr
Sziasztok! Van két random számom [-0.5; 0.5] tartományban (egyenletes eloszlási esélyekkel), és egyedül azt tudom, hogy mi a különbségük abszolút értéke. Szeretnék megállapítani egy felső határt ehhez az értékhez, ami alatt már 90%, hogy a két szám előjele azonos. Mi ez az érték?
-
-
VoidXs
nagyúr
Sziasztok, hogyan lehetne optimálisan megtalálni a szöget két 3D elforgatás közt? Jelenleg azt csinálom, hogy az egységgömbön felveszem a nekik megfelelő pontot, és skalárszorzatból visszaszámolható a szög, ez viszont sok művelet. Lehetne gyorsabban? Az egy könnyítő tényező, hogy az egyik forgatás csak az x, a másik pedig csak az y tengely körül történik, de ezzel is csak a gömbre helyezésből csípek le 1-1 műveletet.
-
VoidXs
nagyúr
válasz
kovisoft
#6220
üzenetére
Köszönöm szépen a választ, ez már sokat segít. Az "összes pont relatív helye" alatt pontosan azt értettem, amit te is. A megoldások közül viszont bármelyik megfelelő, csak algoritmikusan elő lehessen állítani, így a megoldhatóság alatt azt szerettem volna kérdezni, hogy létezik-e olyan módszer, ami garantál bármilyen, a távolsági kritériumoknak megfelelő eredményt. Ha már csak az előállna, hogy 3 pontot tudunk rögzíteni, onnantól körök egyenletével a lehetséges helyeket végig lehet próbálni, és kellően kicsi számoknál (a gyakorlatban 2 <= N <= 8 és 3 <= M <= 21) ezeket még egy egyáltalán nem hatékony algoritmus is gyorsan megtalálja.
-
VoidXs
nagyúr
Sziasztok, egy számomra nehéz feladattal akadtam el, amiről azt se tudom eldönteni, hogy egyáltalán lehetséges-e olyan módon, ami nem brute force. Van két ponthalmazom, és mindkét halmaz pontjairól ismert, hogy a másik halmaz bármely pontjától milyen távol van, de kizárólag ennyi információm van. Meghatározható-e ebből az összes pont relatív helye, és ha igen, hogyan?
-
VoidXs
nagyúr
Sziasztok! Van egy egyszerű trigonometria feladatom, két szakasz hosszát kellene kiszámolni. A probléma ott jön, hogy ez a feladat egy gömbön van rajt, valahogy így:
A zöld és piros ív hosszát szeretném tudni bármely a, b, c, illetve a háromszögön belül felvett r esetén.
Új hozzászólás Aktív témák
- Samsung Galaxy Watch6 Classic - tekerd!
- Renault, Dacia topik
- Milyen széket vegyek?
- Milyen TV-t vegyek?
- bitpork: Phautós tali a Balcsinál 2025 Augusztus 2 napján (szombat)
- Milyen okostelefont vegyek?
- sziku69: Fűzzük össze a szavakat :)
- Luck Dragon: Asszociációs játék. :)
- AMD K6-III, és minden ami RETRO - Oldschool tuning
- PROHARDVER! feedback: bugok, problémák, ötletek
- További aktív témák...
- DDR5 RAMOK
- OHH! Dell Precision 7560 Tervező Vágó Laptop -70% 15,6" i7-11850H 32/1TB NVIDIA A3000 6GB FHD
- Ohh Lenovo ThinkPad P15 G2 Tervező Vágó Laptop -75% 15,6" i5-11500H 32/1TB RTX A2000 4GB /1 Millió/
- LÉZEREZÉS! külföldi billentyűzet magyarra kb. 20-30p alatt!
- Lian Li HydroShift 360 LCD /3x120mm RGB FAN/ HSLCD36RB (593933)
- Bomba ár! Lenovo X1 Yoga 2nd - i7-7G I 8GB I 256SSD I 14" WQHD I HDMI I W11 I CAM I Garancia!
- Xbox Ultimate előfizetések
- Telefon felvásárlás!! Huawei P20 Lite/Huawei P20/Huawei P30 Lite/Huawei P30/Huawei P30 Pro
- BESZÁMÍTÁS! MSI B450M R5 3600 16GB DDR4 512GB SSD GTX 1080 8GB Rampage SHIVA ADATA 600W
- Bomba ár! Dell Latitude E5550 - i5-5GEN I 8GB I 128GB SSD I 15,6" FHD I W10 I HDMI I Cam I Gari!