Hirdetés
Talpon vagyunk, köszönjük a sok biztatást! Ha segíteni szeretnél, boldogan ajánljuk Előfizetéseinket!
Új hozzászólás Aktív témák
-

bundli
tag
válasz
 skoda12
#4433
üzenetére
skoda12
#4433
üzenetére
Na, pár órán át szenvedtem ezzel. Egy baj van evvel a megoldással, hogy az a pont ahova az érintőt húzom, az nem 100%-ig pontos, tehát nincs rajta a parabolán, csak nagyon közel van, mivel közelítéssel számoltam azt.
Így az általad leír módszer nem működik, mert néha negatív a diszkrimináns vagy pedig 0 van a nevezőben, mikor behelyettesítek.
Olyan megoldást kéne találni ami az a,b,c,p,q együtthatókkal számol.
Pl.: Ha a,b és p egyszerre nagyobb mint 0, akkor Y1, egyébként meg Y2-t kell használni.
Csak gondolom ez nem igazán játszik...
-

bundli
tag
válasz
 skoda12
#4431
üzenetére
skoda12
#4431
üzenetére
Az érintő egyenletét a következőképpen számolom.
A derivált Y-ok egyenletébe behelyettesítem az x0-t, ez megad két meredekséget. (m1 vagy m2)
Majd ebbből:
Y1=m1*(x*x0)+y0
Y2=m2*(x*x0)+y0Ez adja meg magát az érintők egyenleteit.
Tehát az egyetlen dolog amivel játszani kell az m, mert abból van kettő.
Namost. Én látom az m-ek értékeit, ezek egymással ellentétes előjelűek. Próbáltam úgy, hogy mindig a negatívat választottam jónak, sajnos ez nem segített.
Te hogyan gondoltam (x0,y0)-ból megmondani, hogy melyik m-et kéne válaszani?
(Elnézést, hogy értetlenkedek, de nagyon fontos lenne nekem és ahogy tudom viszonozni is fogom a segítséget!)
-

bundli
tag
válasz
 skoda12
#4427
üzenetére
skoda12
#4427
üzenetére
Igen, mondjuk ez kirajzoláskor működött is. Viszont miután lederiváltam X szerint a két implicit egyenletet, akkor miután érintőt húztam ezek segítségével a parabola egy pontjába, akkor két egyenesem érintőm lett. Az egyik általában merőleges a másikra. A két egyenes közül az egyik mindig jó, de nem jöttem rá, hogy mikor melyiket kéne kirajzolnom a helyes eredményhez.
Természetesen a parabola helyzettől függ, hogy mikor melyik egyenlet működik.
-

bundli
tag
válasz
 skoda12
#4424
üzenetére
skoda12
#4424
üzenetére
Igen, ez valószínű, hogy a különböző paraméterek értékétől függ, hogy éppen melyik egyenlet az ami fog kelleni nekem. Namost. Hogyan tudom eldönteni mondjuk kirajzoláskor, hogy nekem melyik implicit egyenletbe kell behelyettesíteni?
Ha jól értem, akkor azt az együtthatót kéne vizsgálnom, ami eldönti, hogy most a kettő közül melyik egyenlet lesz a jó. Már csak azt kéne kitalálni hogy hogyan találom meg azt. És mi van ha több is beleszól a dologba egyszerre.

-

bundli
tag
Jönnék akkor mégegy kérdéssel.
Van ez az egyeneletem:
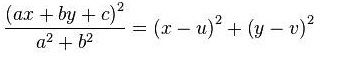
Kifejeztem Y-ra egy matematikai programmal (Matlab), de kettő egyenletet is adott. Ki is próbáltam őket, egyszer vagy az egyikkel adott helyes megoldást, máskor a másikkal. Mitől fordulhatott ez elő? Valaki meg tudja magyarázni, hogy matematikailag melyiket kéne használni és mikor?
-

bundli
tag
Üdv.!
Van ötletetek, hogy hogyan lehet egy parabola egyenletét megkapni 2 pontból és a fókuszponjából?
Tehát 2 pontot lerakok egymás mellé mondjuk, és középre felé egy fókuszpontot. Ebből kéne kiszámolni a parabola egyenletét. Természetesen a 2 pont szimmetrikus a fókuszpontra.
Új hozzászólás Aktív témák
- eBay-es kütyük kis pénzért
- AMD Navi Radeon™ RX 9xxx sorozat
- Kerékpárosok, bringások ide!
- Gaming notebook topik
- NVIDIA GeForce RTX 5070 / 5070 Ti (GB205 / 203)
- ZIDOO médialejátszók
- Milyen légkondit a lakásba?
- Miért álltak az oldalak egy hétig, mi történt?
- Battlefield 6
- Synology NAS
- További aktív témák...
- SzoftverPremium.hu
- BESZÁMÍTÁS! Microsoft XBOX One S 512GB lemezes játékkonzol garanciával hibátlan működéssel
- LG 27GP850P-B - 27" NANO IPS - 2560x1440 - 180Hz 1ms - NVIDIA G-Sync - AMD FreeSync - HDR 400
- GYÖNYÖRŰ iPhone 13 mini 128GB Pink -1 ÉV GARANCIA - Kártyafüggetlen, MS3048, 94% Akkumulátor
- GYÖNYÖRŰ iPhone 11 Pro 64GB Space Grey -1 ÉV GARANCIA - Kártyafüggetlen, MS2052
Állásajánlatok
Cég: FOTC
Város: Budapest








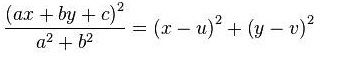
 axioma
axioma
