Hirdetés
Talpon vagyunk, köszönjük a sok biztatást! Ha segíteni szeretnél, boldogan ajánljuk Előfizetéseinket!
Új hozzászólás Aktív témák
-
cucka
addikt
Természetesen elrontottam
Az én képletem és a korábbi képlet ekvivalens egymással. A félreértést az okozza, hogy meg kell különböztetni a korong relatív fordulatszámát és abszolút fordulatszámát. (A relatív fordulatszám az előző koronghoz képest nézett érték, az abszolút pedig egy külső szemlélő által érzékelt érték)Az i. korong abszolut fordulatszáma egyenlő az i-1. korong abszolut fordulatszámának és az i. korong relatív fordulatszámának összegével. (ezt állítottam én)
Az i. korong abszolut fordulatszáma egyenlő az 1., 2., ... i-1., i. korongok relatív fordulatszámának összegével. (ezt mondta a képlet).A fenti két állítás ugyanazt jelenti, csak más formában megfogalmazva. És igen, jól gondolod, ugyanazt mondod, mint amit a fenti állítások megfogalmaznak, csak speciális esetre. (fordulatszám=1)
-
cucka
addikt
Márhogy a képletet hogy értelmezed? A nagy szigma betű n darab összeadást jelöl, a képlet tehát a k(1)+k(2)+.....+k(n) összeget jelenti. (Más szóval a k(i) elemek összege, ahol az i 1 és n közötti természetes szám).
Ezzel a jelöléssel sok helyen találkozhatsz, illetve ennek analógiájára létezik ismételt szorzás (nagy pi-vel jelöljük) vagy ismételt halmazműveletek (nagy únió/metszet jelek).A másik, hogy szerintem a képlet hibás. Egy korong sebessége kizárólag a saját sebességétől és az alatta lévő korong sebességétől függ, tehát ezt a kettőt kell összeadni. Nyilván, a legelső korong alatt nem mozog semmi, tehát ott az alatta lévő korong sebessége nulla.
-
#1804
cucka
addikt
concret_hp
#1803
cucka
addikt
válasz
concret_hp
#1803
üzenetére
Igazából tetszőleges karakterkészlettel és hosszúsággal is könnyen megoldható a feladat, 2 egymásba ágyazott ciklussal. (Vagy ciklus helyett vele ekvivalens rekurzív függvénnyel)
-
cucka
addikt
válasz
petrusz82
#1800
üzenetére
Valami hasonlót (c stílusú nyelvekben valószínűleg működni fog):
unsigned long int i;
for (i=0;i<99999999;i++){
sprintf("%08u\n", i);
}Ez mondjuk a képernyőre írja ki, ezt futtatásnál átirányíthatod file-ba, esetleg használhatod az fprintf függvényt. (C++-ban van ilyen, php-ban is, gondolom más nyelvekben is megoldható). Az sprintf-ben a %u azt jelenti, hogy oda a paraméterként kapott i természetes számot fogja bepakolni, előtte a 08 azt jelenti, hogy 8 karakter szélességben szeretnéd az eredményt, balról 0-kkal kitöltve, a \n pedig a sortörés. Windows-os sortöréshez a \r\n-t használd, MacOS-en pedig a \r-t.
Amúgy az eredményül kapott file windows-on 900 MB-ot fog foglalni. (Windows-os sorvégekkel 1000MB). Ha tetszőlegesen hosszú számokra is működnie kell, akkor bonyolultabb a megoldás, bár sok értelme nem lenne . -
#1648
cucka
addikt
philoxenia
#1642
cucka
addikt
válasz
philoxenia
#1642
üzenetére
Lehet, hogy valamit félreértettem, de itt annyi elég, ha minden rab átkapcsolja a lámpát amennyiben először van kinn sétálni. Ezután már csak számolgatni kell az átkapcsolásokat
. -
cucka
addikt
válasz
MiaCica
#1417
üzenetére
Milyen hosszú az oldala ?
2. A szabályos négyoldalú gúla alapéle a, magassága h.
1. Lerajzolod a gúlát.
2. Belerajzolod a magasságot.
3. A magasság alapját összekötöd az alap négyzet egyik csúcsával.
4. Kapsz egy derékszögű háromszöget a következő oldalakkal:
- a magasság
- az alap átlójának fele
- a gúla oldala
Az első két oldal hosszát tudod, a harmadikat pitagorasz tétellel kiszámolod.4. Az a,b és c pozitív számok egy számtani és ugyanakkor egy mértani sorozat m-edik, n-edik és p-edik tagjai...
Ezt nem fogom végigszámolni, gondolom fel kell írni az a,b,c értékeket számtani és mértani sorozat x. tagjaként és behelyettesíteni a végső képletbe. Lesz két egyenleted, ezeket kell úgy masszírozni, hogy kijöjjön az eredmény. (Valószínűleg ki kell majd vonni a két egyenletet egymásból, hogy a jobb oldalon 0 legyen, és ki kell hozni a bal oldalt is nullára.) -
-
#1296
cucka
addikt
MR. Anderson
#1292
cucka
addikt
válasz
MR. Anderson
#1292
üzenetére
Amúgy ebben mi a nehéz? Egyetlen fontos és hasznos képlet van a számtani sorozatoknál, ami a számtani sorozat i. tagjának értékét adja meg az első első tagja és a differencia függvényében:
a(i)=a(1)+d*(i-1)
A feladatokban megkapott adatokat behelyettesíted a képletbe, kapsz egy hihetetlenül bonyolult elsőfokú egyismeretlenes egyenletet, amit meg kell oldani, ennyi az egész. Melyik résszel voltak problémáid?
Ok, a második feladatodnál két egyenlet van, amit ki kell vonni egymásból.
-
cucka
addikt
Így utólag belegondolva rájöttem, hogy elrontottam.
A következő állítás sajnos nem igaz: A beírt henger térfogata akkor a legnagyobb, ha a keresztmetszeténeka területe a legnagyobb. . Azért nem igaz, mert a térfogat a magasságtól és a sugár négyzetétől függ.
Addig ok, hogy kifejezed a henger magasságát és sugarát a-val.
Erre felírod a henger térfogatképletét:
V=pi*(1-a)*m*a^2*r^2
Ezt kell a szerint deriválni
V'=2*a*c-3*a^2*c, ahol c=m*pi*r^2
A V' 0 és 2/3 pontokban veszi fel a nullát, 0<a<1 feltétel miatt a=2/3 -
cucka
addikt
Jól látod, valóban deriválással kell, és jól látod, valóban az a feladattal a probléma, hogy kitaláld, mit kell deriválni.
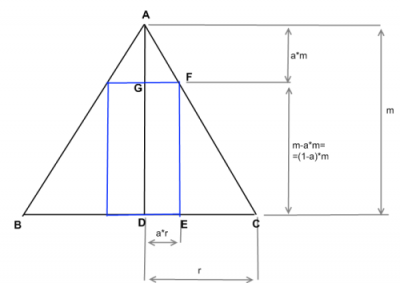
Első lépés, hogy elmetszed a kúpot, mert síkban jobb dolgozni, mint térben. A beírt henger térfogata akkor a legnagyobb, ha a keresztmetszeténeka területe a legnagyobb.Csatoltam egy képet, kékkel jelölve a beírt henger keresztmetszetét. Elég az ADC háromszögben dolgozni, tehát a kérdés, hogy a DEFG téglalap területe mikor maximális.
Legyen DE=a*r, ahol 0<a<1. AGF és ADC háromszögek hasonlóak, emiatt oldalaik hossza arányos, tehát DE=a*DC-ből következik, hogy AG=a*AD=a*m. Innen GD=m-a*m=m*(1-a).
DEFG területe GD*DE=a*r*(m-a*m)=r*m*(-a^2+a). Az r és m értékei fixek, tehát ez akkor lesz a legnagyobb, ahol a -a^2+a függvény felveszi a maximumát. Deriválással megkapod, hogy a függvénynek a=1/2 pontban van a maximuma és kész is vagy.
-
cucka
addikt
Valóban, átsiklottam fölötte.
Amit mondjuk helytelenítek (de sajnos Magyarországon így tanítják), hogy mindenféle hülye számokkal kell számolni, számológéppel. Most komolyan, kit érdekel, hogy mennyi a sin(54fok)? Az ilyenek vezetik rá a diákokat a számológéppel való számolásra. Nálunk matekórán az ilyen hülyeségeket soha nem számoltuk ki, ha valamit nagyon muszáj volt, akkor azt viszont kézzel kellett, szorozni/osztani tudni kellett számológép nélkül is. -
cucka
addikt
válasz
TexT-BoY
#1088
üzenetére
Az első feladatot jó szarul oldottad meg
A rajzodon ismered a gamma szövet (36 vagy 54 fok, teljesen mindegy, melyikkel számolsz).
Tudod a szög szinuszát és koszinuszát, mert megmondja a számológép.
Tudod, hogy sin(gamma)=szöggel szembeni befogó / átfogó
Tudod, hogy cos(gamma)=szög melletti befogó / átfogó
Utóbbi kettő egyenletből egy keresztbe szorzással megvan a két oldal. Fölösleges idekeverni az átlók metszéspontjánál létrejövő szögeket..
Annyi a mentségem, hogy szabályos tetraéderrel is a vázolt módon kell megcsinálni a feladatot.
Új hozzászólás Aktív témák
axioma
- Gamer PC- Számítógép! Csere-Beszámítás! I5 12400F / RTX 3070 8GB / 32GB DDR4 / 500GB SSD+ 2TB HDD
- Telefon felvásárlás!! iPhone 14/iPhone 14 Plus/iPhone 14 Pro/iPhone 14 Pro Max
- Telefon felvásárlás!! iPhone 13 Mini/iPhone 13/iPhone 13 Pro/iPhone 13 Pro Max
- LG 34WQ75X-B - 34" Ívelt IPS Panel - 3440x1440 2K QHD - 60Hz 5ms - FreeSync - USB Type-C 90W
- BESZÁMÍTÁS! Asus TUF A620M R7 7700 32GB DDR5 1TB SSD RX 6800 XT 16GB ZALMAN I3 NEO Gigabyte 750W
Állásajánlatok
Cég: FOTC
Város: Budapest