- Honor 400 Pro - gép a képben
- Mi nincs, grafén akku van: itt a Xiaomi 11T és 11T Pro
- Csak semmi szimmetria: flegma dizájnnal készül a Nothing Phone (3)
- Vivo V40 5G - az első benyomás fontos
- Vivo X200 Pro - a kétszázát!
- Samsung Galaxy A56 - megbízható középszerűség
- Android alkalmazások - szoftver kibeszélő topik
- CMF Buds Pro 2 - feltekerheted a hangerőt
- iPhone topik
- Samsung Galaxy Watch7 - kötelező kör
Aktív témák
-
#55
t3rm1nat0r
csendes tag
t3rm1nat0r
#54
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#54
üzenetére
Igy nem villog annyira.
XFlush(disp);
usleep(10000); -
#53
t3rm1nat0r
csendes tag
t3rm1nat0r
#52
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#52
üzenetére
Az idézet innen ered.
http://current.com/items/90598372_genius-one-percent-inspiration-99-percent-grit.htm
-
#50
t3rm1nat0r
csendes tag
t3rm1nat0r
#49
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#49
üzenetére
Az eredmény magáért beszél.
A csővezetékkel párhuzamosan futnak a véletlenszerűen kiválasztott értékek, amiket össze kell majd szorozni.
Itt már látható a vektorprocesszor üresjárata. Nem ad eredményt addig, míg fel nem töltődik adattal. Pedig a 128. elemtől kezdem, ami az első két véletlen szám helye. Azért nem nullától, mert a pipelineban visszafele vannak az értékek. Előrébb vannak, amik régebben belekerültek.
De amikor az első adat elérte a csővezeték végét, utánna már minden ciklusban kapok egy eredményt.0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0000000000000000= 0 cr= 0 0 * 0 = 0
0100111110101010= 20394 cr= 0 103 * 198 = 20394
0010111100101011= 12075 cr= 0 105 * 115 = 12075
0101000010101111= 20655 cr= 0 81 * 255 = 20655
0100010000111000= 17464 cr= 0 74 * 236 = 17464
0010000011010101= 8405 cr= 0 41 * 205 = 8405
0111110000111110= 31806 cr= 0 186 * 171 = 31806
1110110101000110= 60742 cr= 0 242 * 251 = 60742
0011111000010010= 15890 cr= 0 227 * 70 = 15890
0101110111111000= 24056 cr= 0 124 * 194 = 24056
0101000101100000= 20832 cr= 0 84 * 248 = 20832
0001100001111000= 6264 cr= 0 27 * 232 = 6264
0111111100111011= 32571 cr= 0 231 * 141 = 32571
0010100101111100= 10620 cr= 0 118 * 90 = 10620
0001000111001010= 4554 cr= 0 46 * 99 = 4554
0001111110101101= 8109 cr= 0 51 * 159 = 8109
0111100011101010= 30954 cr= 0 201 * 154 = 30954
0001001111101100= 5100 cr= 0 102 * 50 = 5100
0000100101001011= 2379 cr= 0 13 * 183 = 2379
0001000011011000= 4312 cr= 0 49 * 88 = 4312
0011100101001110= 14670 cr= 0 163 * 90 = 14670
0000110101110001= 3441 cr= 0 37 * 93 = 3441
0000000001110011= 115 cr= 0 5 * 23 = 115
0101000000011000= 20504 cr= 0 88 * 233 = 20504
0100110111011000= 19928 cr= 0 94 * 212 = 19928
0111011011100110= 30438 cr= 0 171 * 178 = 30438
1001111010001110= 40590 cr= 0 205 * 198 = 40590
0110110011111100= 27900 cr= 0 155 * 180 = 27900
0000010110010100= 1428 cr= 0 84 * 17 = 1428
0000011100011100= 1820 cr= 0 14 * 130 = 1820
0001110101110100= 7540 cr= 0 116 * 65 = 7540
0000011111011101= 2013 cr= 0 33 * 61 = 2013
0111010000000100= 29700 cr= 0 220 * 135 = 29700
0110010111110000= 26096 cr= 0 112 * 233 = 26096
0010011011111110= 9982 cr= 0 62 * 161 = 9982
0011100100100001= 14625 cr= 0 65 * 225 = 14625
0110010101100100= 25956 cr= 0 252 * 103 = 25956
0000000000111110= 62 cr= 0 62 * 1 = 62
0100101001010010= 19026 cr= 0 126 * 151 = 19026
1100100100011000= 51480 cr= 0 234 * 220 = 51480
0011111010110010= 16050 cr= 0 107 * 150 = 16050
0001111101001000= 8008 cr= 0 143 * 56 = 8008
0000111100011000= 3864 cr= 0 92 * 42 = 3864
1010001001000000= 41536 cr= 0 236 * 176 = 41536
0011100111011001= 14809 cr= 0 59 * 251 = 14809
0010001000101110= 8750 cr= 0 50 * 175 = 8750
0001001110110000= 5040 cr= 0 60 * 84 = 5040
0001011000100000= 5664 cr= 0 236 * 24 = 5664
0100111010110100= 20148 cr= 0 219 * 92 = 20148
0000000000110100= 52 cr= 0 2 * 26 = 52
0100001001111010= 17018 cr= 0 254 * 67 = 17018
1111010100011110= 62750 cr= 0 251 * 250 = 62750
0010011010000100= 9860 cr= 0 170 * 58 = 9860
0010100000110011= 10291 cr= 0 251 * 41 = 10291
1011101111000110= 48070 cr= 0 209 * 230 = 48070
0000000100101100= 300 cr= 0 5 * 60 = 300
0100011110110000= 18352 cr= 0 124 * 148 = 18352
0110001010111000= 25272 cr= 0 117 * 216 = 25272
0100011111111110= 18430 cr= 0 190 * 97 = 18430
1000010101000001= 34113 cr= 0 137 * 249 = 34113
0100001100110100= 17204 cr= 0 92 * 187 = 17204
0110010001101000= 25704 cr= 0 168 * 153 = 25704
0000100010111011= 2235 cr= 0 15 * 149 = 2235
1010001001111011= 41595 cr= 0 177 * 235 = 41595
1010100010000011= 43139 cr= 0 241 * 179 = 43139
0000010010101011= 1195 cr= 0 5 * 239 = 1195 -
#49
t3rm1nat0r
csendes tag
t3rm1nat0r
#48
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#48
üzenetére
De ha már belekezdtem, akkor legyen itt a teljes szorzo.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int pipeline[128][32];
int parameter[256][2][8],szam[256][2];
int adder_tablazat[4*4*2][4];
int main()
{
int c,i,j,k,l,mask;
for(c=0;c<2;c++)//carry
for(i=0;i<4;i++)
for(j=0;j<4;j++)
{
int osszeg=i+j+c;
int addr=c*16+i*4+j;
mask=1;
for(k=0;k<3;k++) {adder_tablazat[addr][k]=((osszeg & mask)>>k);mask<<=1;}
}
for(c=0;c<2;c++)//carry
for(i=0;i<4;i++)
for(j=0;j<4;j++)
{
int osszeg=i+j+c;
mask=1;
printf("%d + %d + %d =%d ",i,j,c,osszeg);
for(k=0;k<3;k++) printf("%d",adder_tablazat[c*16+i*4+j][2-k]);
printf("\n");
}
for(j=128;j<256;j++)//eleje ures
{
szam[j][0]=rand()%256;//veletlen ertekeket szoroz ossze
szam[j][1]=rand()%256;
mask=1;
for(k=0;k<8;k++) {parameter[j][0][k]=(szam[j][0] & mask)>>k;mask<<=1;}
mask=1;
for(k=0;k<8;k++) {parameter[j][1][k]=(szam[j][1] & mask)>>k;mask<<=1;}
}
int pl=8*8+1;
int plp=128;//elso elem
for(l=0;l<pl*2;l++)//ciklus
{
//if(l==pl-1)//csak a vegen irja ki
{
// for(j=0;j<pl;j++)
j=pl;
{
mask=0x8000;
int bits=0;
for(k=0;k<16;k++)
{
int bit=pipeline[j][15-k];
printf("%d",bit);
if(bit) bits|=mask;
mask>>=1;
}
printf("= %d ",bits);
printf(" cr= %d ",pipeline[j][20]);
int p=(plp-j);
printf("%d * %d = %d ",szam[p][0],szam[p][1],szam[p][0]*szam[p][1]);
}
printf("\n");
}
mask=1;
for(k=0;k<32;k++) pipeline[0][k]=0;//mindig nullaval kezd
int plp2=plp-pl;
plp++;
for(j=pl;j>=0;j--)//csovezetek
{
int j2=j&7;//8 16-bites adder
int bit_offset=j>>3;
int p=plp2;
plp2++;//a kovetkezo fokozatban regebbi van,j visszafele megy
for(k=0;k<16;k+=2)
{
if((k>>1) == j2 )
{
int bita0=pipeline[j][k];
int bita1=pipeline[j][k+1];
int bitb0=0;
int bitb1=0;
int carry=pipeline[j][20];
if(j2==0) carry=0;//adder start
int d=k-bit_offset;
if(d>=0 && d<8) bitb0=parameter[p][1][d];
d++;
if(d>=0 && d<8) bitb1=parameter[p][1][d];
if(parameter[p][0][bit_offset]==0) //0-val szoroz
{
bitb0=0;
bitb1=0;
}
int addra=(bita1<<1)+bita0;
int addrb=(bitb1<<1)+bitb0;
addra=(carry<<4) + (addra<<2) + addrb;
pipeline[j+1][k ]=adder_tablazat[addra][0];
pipeline[j+1][k+1]=adder_tablazat[addra][1];
pipeline[j+1][20 ]=adder_tablazat[addra][2];//carry
}
else
{
pipeline[j+1][k] =pipeline[j][k];
pipeline[j+1][k+1]=pipeline[j][k+1];
}
}
}
}
return 0;
} -
#48
t3rm1nat0r
csendes tag
t3rm1nat0r
#47
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#47
üzenetére
Ez még nem a teljes megoldás.
Ahhoz a parameter[] tömbből is csővezetéket kell építeni, ekkor a szam1 és a szam2 minden ciklusban más értékű lehet.
A vektorprocesszor lényegét akartam megmutatni, és az így jobban látszik, nincs túlbonyolítva az egész. -
#47
t3rm1nat0r
csendes tag
t3rm1nat0r
#46
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#46
üzenetére
A kimenő értékek.
135 * 212 = 28620
0 + 0 + 0 =0 000
0 + 1 + 0 =1 001
0 + 2 + 0 =2 010
0 + 3 + 0 =3 011
1 + 0 + 0 =1 001
1 + 1 + 0 =2 010
1 + 2 + 0 =3 011
1 + 3 + 0 =4 100
2 + 0 + 0 =2 010
2 + 1 + 0 =3 011
2 + 2 + 0 =4 100
2 + 3 + 0 =5 101
3 + 0 + 0 =3 011
3 + 1 + 0 =4 100
3 + 2 + 0 =5 101
3 + 3 + 0 =6 110
0 + 0 + 1 =1 001
0 + 1 + 1 =2 010
0 + 2 + 1 =3 011
0 + 3 + 1 =4 100
1 + 0 + 1 =2 010
1 + 1 + 1 =3 011
1 + 2 + 1 =4 100
1 + 3 + 1 =5 101
2 + 0 + 1 =3 011
2 + 1 + 1 =4 100
2 + 2 + 1 =5 101
2 + 3 + 1 =6 110
3 + 0 + 1 =4 100
3 + 1 + 1 =5 101
3 + 2 + 1 =6 110
3 + 3 + 1 =7 111
0000000000000000= 0 cr= 0
0000000000000000= 0 cr= 0
0000000000000100= 4 cr= 0
0000000000010100= 20 cr= 0
0000000011010100= 212 cr= 0
0000000011010100= 212 cr= 0
0000000011010100= 212 cr= 0
0000000011010100= 212 cr= 0
0000000011010100= 212 cr= 0
0000000011010100= 212 cr= 0
0000000011011100= 220 cr= 0
0000000011111100= 252 cr= 0
0000000001111100= 124 cr= 1
0000001001111100= 636 cr= 0
0000001001111100= 636 cr= 0
0000001001111100= 636 cr= 0
0000001001111100= 636 cr= 0
0000001001111100= 636 cr= 0
0000001001111100= 636 cr= 0
0000001001001100= 588 cr= 1
0000001011001100= 716 cr= 0
0000000111001100= 460 cr= 1
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000010111001100= 1484 cr= 0
0000011111001100= 1996 cr= 0
0000111111001100= 4044 cr= 0
0010111111001100= 12236 cr= 0
0110111111001100= 28620 cr= 0 -
#46
t3rm1nat0r
csendes tag
t3rm1nat0r
#45
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#45
üzenetére
..és íme a csoda..
ehhez hasonlóan dolgozik a geforce/ati-nk.#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int pipeline[128][32];
int parameter[2][8];
int adder_tablazat[4*4*2][4];
int main()
{
int c,i,j,k,l,mask,szam1=135,szam2=212;
printf("%d * %d = %d\n",szam1,szam2,szam1*szam2);
for(c=0;c<2;c++)//carry
for(i=0;i<4;i++)
for(j=0;j<4;j++)
{
int osszeg=i+j+c;
int addr=c*16+i*4+j;
mask=1;
for(k=0;k<3;k++) {adder_tablazat[addr][k]=((osszeg & mask)>>k);mask<<=1;}
}
for(c=0;c<2;c++)//carry
for(i=0;i<4;i++)
for(j=0;j<4;j++)
{
int osszeg=i+j+c;
mask=1;
printf("%d + %d + %d =%d ",i,j,c,osszeg);
for(k=0;k<3;k++) printf("%d",adder_tablazat[c*16+i*4+j][2-k]);
printf("\n");
}
mask=1;
for(k=0;k<8;k++) {parameter[0][k]=(szam1 & mask)>>k;mask<<=1;}
mask=1;
for(k=0;k<8;k++) {parameter[1][k]=(szam2 & mask)>>k;mask<<=1;}
mask=1;
for(k=0;k<32;k++) pipeline[0][k]=0;//carry + nullaval kezd
int pl=8*8+1;
for(l=0;l<pl;l++)
{
if(l==pl-1)//csak a vegen irja ki
{
for(j=0;j<pl;j++)
{
mask=0x8000;
int bits=0;
for(k=0;k<16;k++)
{
int bit=pipeline[j][15-k];
printf("%d",bit);
if(bit) bits|=mask;
mask>>=1;
}
printf("= %d ",bits);
printf(" cr= %d\n",pipeline[j][20]);
}
printf("\n");
}
for(j=pl;j>=0;j--)
{
int j2=j&7;//8 16-bites adder
int bit_offset=j>>3;
for(k=0;k<16;k+=2)
{
if((k>>1) == j2 )
{
int bita0=pipeline[j][k];
int bita1=pipeline[j][k+1];
int bitb0=0;
int bitb1=0;
int carry=pipeline[j][20];
if(j2==0) carry=0;//adder start
int d=k-bit_offset;
if(d>=0 && d<8) bitb0=parameter[1][d];
d++;
if(d>=0 && d<8) bitb1=parameter[1][d];
if(parameter[0][bit_offset]==0) //0-val szoroz
{
bitb0=0;
bitb1=0;
}
int addra=(bita1<<1)+bita0;
int addrb=(bitb1<<1)+bitb0;
addra=(carry<<4) + (addra<<2) + addrb;
pipeline[j+1][k ]=adder_tablazat[addra][0];
pipeline[j+1][k+1]=adder_tablazat[addra][1];
pipeline[j+1][20 ]=adder_tablazat[addra][2];//carry
}
else
{
pipeline[j+1][k] =pipeline[j][k];
pipeline[j+1][k+1]=pipeline[j][k+1];
}
}
}
}
return 0;
} -
#44
t3rm1nat0r
csendes tag
t3rm1nat0r
#43
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#43
üzenetére
61 + 35 = 96
0 + 0 + 0 =0 000
0 + 1 + 0 =1 001
0 + 2 + 0 =2 010
0 + 3 + 0 =3 011
1 + 0 + 0 =1 001
1 + 1 + 0 =2 010
1 + 2 + 0 =3 011
1 + 3 + 0 =4 100
2 + 0 + 0 =2 010
2 + 1 + 0 =3 011
2 + 2 + 0 =4 100
2 + 3 + 0 =5 101
3 + 0 + 0 =3 011
3 + 1 + 0 =4 100
3 + 2 + 0 =5 101
3 + 3 + 0 =6 110
0 + 0 + 1 =1 001
0 + 1 + 1 =2 010
0 + 2 + 1 =3 011
0 + 3 + 1 =4 100
1 + 0 + 1 =2 010
1 + 1 + 1 =3 011
1 + 2 + 1 =4 100
1 + 3 + 1 =5 101
2 + 0 + 1 =3 011
2 + 1 + 1 =4 100
2 + 2 + 1 =5 101
2 + 3 + 1 =6 110
3 + 0 + 1 =4 100
3 + 1 + 1 =5 101
3 + 2 + 1 =6 110
3 + 3 + 1 =7 111
00100011= 35 cr= 0
00000000= 0 cr= 0
00000000= 0 cr= 0
00000000= 0 cr= 0
00000000= 0 cr= 000100011= 35 cr= 0
00100000= 32 cr= 1
00001100= 12 cr= 0
00110000= 48 cr= 0
00000000= 0 cr= 000100011= 35 cr= 0
00100000= 32 cr= 1
00100000= 32 cr= 1
00111100= 60 cr= 0
00110000= 48 cr= 000100011= 35 cr= 0
00100000= 32 cr= 1
00100000= 32 cr= 1
00100000= 32 cr= 1
00111100= 60 cr= 000100011= 35 cr= 0
00100000= 32 cr= 1
00100000= 32 cr= 1
00100000= 32 cr= 1
01100000= 96 cr= 0Mint látható, helyes eredmény ad, jó kiindulási alap lesz a szorzáshoz.
Az elején az összeadás azért van, hogy lehessen látni, melyik számnak kell kijönnie itt a csővezeték végén.Az elején kiirattam a 2x2x1 bites összeadó táblát is. Igy a legegyszerűbb és a leggyorsabb összeadni, hiszen csak ki kell emelni a memóriából az eredményt.
Az igazi az lenne, ha két 64 bites szám összes összegét le lehetne tárolni, de ez nyilván lehetetlen, mert hatalmas memória kellene hozzá.
-
#43
t3rm1nat0r
csendes tag
t3rm1nat0r
#42
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#42
üzenetére
..és a teljes program..
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int pipeline[8*4][9];
int parameter[8];
int adder_tablazat[4*4*2][4];
int main()
{
int c,i,j,k,l,mask,szam1=61,szam2=35;
printf("%d + %d = %d\n",szam1,szam2,szam1+szam2);
for(c=0;c<2;c++)//carry
for(i=0;i<4;i++)
for(j=0;j<4;j++)
{
int osszeg=i+j+c;
int addr=c*16+i*4+j;
mask=1;
for(k=0;k<3;k++) {adder_tablazat[addr][k]=((osszeg & mask)>>k);mask<<=1;}
}
for(c=0;c<2;c++)//carry
for(i=0;i<4;i++)
for(j=0;j<4;j++)
{
int osszeg=i+j+c;
mask=1;
printf("%d + %d + %d =%d ",i,j,c,osszeg);
for(k=0;k<3;k++) printf("%d",adder_tablazat[c*16+i*4+j][2-k]);
printf("\n");
}
mask=1;
for(k=0;k<8;k++) {parameter[k]=(szam1 & mask)>>k;mask<<=1;}
mask=1;
for(k=0;k<8;k++) {pipeline[0][k]=(szam2 & mask)>>k;mask<<=1;}
pipeline[0][8]=0;//carry
int pl=4+1;
for(l=0;l<pl;l++)
{
for(j=0;j<pl;j++)
{
mask=0x80;
int bits=0;
for(k=0;k<8;k++)
{
int bit=pipeline[j][7-k];
printf("%d",bit);
if(bit) bits|=mask;
mask>>=1;
}
printf("= %d ",bits);
printf(" cr= %d\n",pipeline[j][8]);
}
printf("\n");
for(j=pl;j>=0;j--)
for(k=0;k<8;k+=2)
{
if((k>>1) == j)
{
int bita0=pipeline[j][k];
int bita1=pipeline[j][k+1];
int bitb0=parameter[k];
int bitb1=parameter[k+1];
int carry=pipeline[j][8];
int addra=(bita1<<1)+bita0;
int addrb=(bitb1<<1)+bitb0;
addra=(carry<<4) + (addra<<2) + addrb;
pipeline[j+1][k ]=adder_tablazat[addra][0];
pipeline[j+1][k+1]=adder_tablazat[addra][1];
pipeline[j+1][8 ]=adder_tablazat[addra][2];//carry
}
else
{
pipeline[j+1][k] =pipeline[j][k];
pipeline[j+1][k+1]=pipeline[j][k+1];
}
}
}
return 0;
} -
#41
t3rm1nat0r
csendes tag
t3rm1nat0r
#40
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#40
üzenetére
Lehet tanulni sőt kell is, de nincs hatékonyabb módszer annál, mint amit a saját tapasztalat alakít ki.
-
#40
t3rm1nat0r
csendes tag
t3rm1nat0r
#39
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#39
üzenetére
Látszólag van egy hiba, amihez nekem is idő kellett míg rájöttem, hogy nem is hiba.
Néha a számsorban egy-két szám értéke nagyon leesik.
Ennek egyszerű oka van, néha a "bentrekedt" átvitel nem látszik, csak a következő fokozatban adódik a számhoz.Ez a vektorprocesszor titka. Itt jól látszik az is amiről már írtam.
Az első eredmény megjelenéséig fel kell tőltődnie minden fokozatnak.
Ha ezer fokozat van, akkor ezer cikluson keresztül nincs eredmény. De utánna minden ciklusban kapunk egy kiszámolt értéket. -
#39
t3rm1nat0r
csendes tag
t3rm1nat0r
#38
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#38
üzenetére
A kimenet ez, ha 00001010-at ad a counter aktuális értékéhez.
00000101 = 5
00000110 = 6
00001101 = 13
00001100 = 12
00001011 = 1100000110 = 6
00000111 = 7
00001110 = 14
00001101 = 13
00001100 = 12Látszólag összevissza számok vannak idedobálva. Az első a counter értéke, az utanná levő számok a pipeline 4 elemének értékei. Amikor a counter 5, akkor a csővezetékben 4,3,2,1- es értékek kerültek. Azért nem ezeket az értékeket látjuk, mert fokozatosan hozzáadódnak a 00001010 bitjei. Először a legalsó kettő, majd kettessével tovább.
Az utolsó fokozat 11, ami megfelel az 1+10 összegnek.
Ha nullát adok a counterhez, akkor jobban látszik, hogy mennek a számok a pipeline-ban végig.Azért két bitet adok össze egy fokozatban, mert a képernyőre nem fér ki több kapu. De lehet próbálkozni. Igazából kétszer álltam neki, de az első PRÓBÁLKOZÁSOM teljesen hibás értékeket adott, úgyhogy teljesen újrakezdtem az egészet.
Dehát az ember már csak ilyen, próbálkozik, és nem adja fel.
Soha. -
#37
t3rm1nat0r
csendes tag
t3rm1nat0r
#22
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#22
üzenetére
Van néhány rész a programban, ami nem egyértelmű, miért van úgy megvalósítva.
Az egyik a define_dflip() függvényben minden define_links() utolsó paramétere 1 vagy nulla. Ha lekövetjük, akkor látható, hogy ez a nand[t].out=default_out; sort fogja vezérelni, ami a kezdő kimeneti állapotot állítja be.
Miért kell ez? Az ok egyszerű, nincs reset a D-flipfloppokon, és ezeknek van egy olyan rossz tulajdonságuk, hogy néha nemdefiniált állapotba kerülnek. Ez elkerülhető ha egyből stabil állapotba állítom mindet.
-
#35
t3rm1nat0r
csendes tag
t3rm1nat0r
#18
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#18
üzenetére
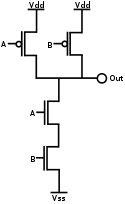
CMOS NAND gate
-
#32
t3rm1nat0r
csendes tag
t3rm1nat0r
#25
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#25
üzenetére
Mint kivehető a képből, négy bemeneti vezetékből 16 kimenetet állít elő.
Mármint a programból. A képen csak egy 3-8 -as dekóder van.
-
#31
t3rm1nat0r
csendes tag
t3rm1nat0r
#20
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#20
üzenetére
ROTATE LEFT
Ahogy elnézem, ez inkább SHIFT LEFT lesz. Forgatásnál a bitek visszaforognak.A teljes skála
http://www.osdata.com/topic/language/asm/shiftrot.htm -
#30
t3rm1nat0r
csendes tag
t3rm1nat0r
#27
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#27
üzenetére
/a getchar();-hoz a konzolon kell nyomni egy entert /
-
#29
t3rm1nat0r
csendes tag
t3rm1nat0r
#24
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#24
üzenetére
A dekóder értékének a kiiratása felesleges. Szemmel jól látszik, ahogy mindig csak egy jobb oldali NAND kapunak 1 a kimenete.
Ez címezhetne egy ramban egy sor kondenzátort, ami tartalmazhatna egy egyszerű utasítást. Azt lehetne dekódolni, egyszerű összeadásra és forgatásokra.De ahhoz már nagyobb hely kellene, így ez egyenlőre ennyi.
-
#27
t3rm1nat0r
csendes tag
t3rm1nat0r
#24
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#24
üzenetére
A legalsó kép két bitet és egy átvitelt ad össze, az eredmény 1 bit és egy új átvitel.
Ez 8 bites összeadónál annyit jelent, hogy miután beálltak stabil állapotba az első bitösszeadó kapui, a következő bit ekkor kapja meg az átvitelt.
Igaz hogy addig az is beállt valahogy, de az az eredmény érvénytelen, hiszen az első bitösszeadó áltvitel bitje csak most lett "érvényes".Ezt a "beállást" nagyon szépen látni lehet a programban, ha kissé módosítjuk.
draw_layer();//ido kell mig minden beall, kirajzolhato a koztes allapot
//ide meg lehetne tenni valamilyen Sleep(x)-et
//getchar();Ezt a két sort módosítva látható, ahogy végighullámzik ez a beállás a tranzisztorokon. Ezért /is/ lassúak viszonylag a hagyományos processzorok. Az átvitelbitnek végig kell futnia az összeadón. És a szorzásról még nem is beszéltem. /Nem is fogok. xD/
A vektorprocesszorok ezt úgy oldják meg /Cray, geforce, etc/, hogy egy órajelciklus alatt csak egyetlen bitet adnak össze egy számon. A többi bit közben csak tárolódik, mondjuk egy flipflop sorban. Az átvitel a következő fozokatban adódik majd hozzá a számhoz, miközben az előző fokozat sem megy üresjáratban, hanem oda már egy másik szám érkezett. Könnyen belátható, hogy így nincs "beállási hullám", és minden ciklusban helyes eredmény kapunk.
Az egyetlen hátránya a dolognak, hogy a "vektor csővezetéket" fel kell tölteni, addig csak üresjáratban fut. Nincs értelme egyetlen számmal műveletet végezni, csak és kizárólag nagy tömbökkel. -
#25
t3rm1nat0r
csendes tag
t3rm1nat0r
#24
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#24
üzenetére
Talán kezdem a decoderrel.
Mint kivehető a képből, négy bemeneti vezetékből 16 kimenetet állít elő. Helyesebben a 16 közül mindig csak egy aktív. A 4 vezeték egy 4 bites decimális számként van értelmezve. A 16 vezeték közül mindig az aktív, amelyik sorszáma megfelel a deciális szám értékének.
Az első lépés, hogy a 4 vezeték invertálódik. Ez azért kell mert mint mostmár tudjuk, az AND kapu akkor fog aktíválódni, ha minden bemenete 1. Itt négy bemenetű AND kapuk vannak a képen. Ezért nem kell megtanulni a táblázatot, elég csak a szabályt alkalmazni. 1000 bemenetű AND kapura is az érvényes.
Tehát a 10 érteknél a vezetéken 1010 érték lesz. A két nullás vezetéknek az inverzét kell venni, így kapjuk az 1111 értéket, ami már aktíválni fogja az AND kaput.void define_decoder(int tr3,int tr4,int mask)
{
int dx[]={sor,sor,sor,sor};//invertalva egy ketsorral lejjebbif(mask&1) dx[0]=0;
if(mask&2) dx[1]=0;
if(mask&4) dx[2]=0;
if(mask&8) dx[3]=0;define_links(tr3 ,tr4+dx[0] ,tr4+ketsor+dx[1],0);
define_links(tr3+1,tr3,link_5V,0); //inverterdefine_links(tr3+2,tr4+ketsor*2+dx[2],tr4+ketsor*3+dx[3],0);
define_links(tr3+3,tr3+2,link_5V,0);//inverterdefine_links(tr3+4,tr3+1,tr3+3,0);
define_links(tr3+5,tr3+4,link_5V,0);//inverter
}/A programban nincs szükség invertálásra, mert a decoder a counter-t dekódolja, ami Dflipfloppokból áll. Azokról pedig közvetlenül levehető a kimenet inverze, hiszen a visszacsatolt rész pont így működik./
-
#24
t3rm1nat0r
csendes tag
t3rm1nat0r
#23
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#23
üzenetére
A program már tartalmazza a cím dekódolót és az összeadót is. Ezek így néznek ki.
-
#19
t3rm1nat0r
csendes tag
t3rm1nat0r
#18
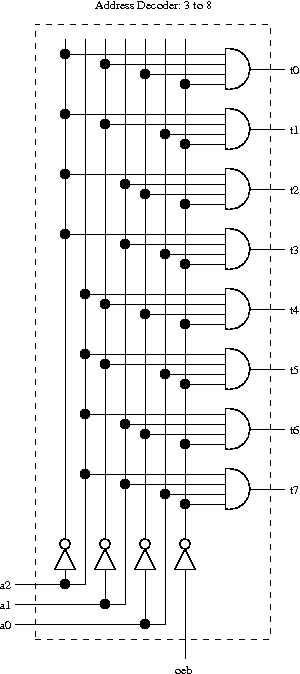
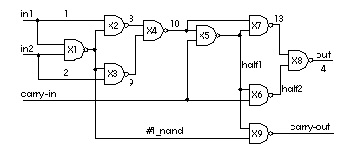
t3rm1nat0r
csendes tag
válasz
t3rm1nat0r
#18
üzenetére
A linkbe került egy smile-vezérlő karakter, de jó a link.
Aktív témák
Hirdetés
- Milyen billentyűzetet vegyek?
- Honor 400 Pro - gép a képben
- Mi nincs, grafén akku van: itt a Xiaomi 11T és 11T Pro
- Kerékpárosok, bringások ide!
- Soundbar, soundplate, hangprojektor
- Vezetékes FEJhallgatók
- Óra topik
- AMD K6-III, és minden ami RETRO - Oldschool tuning
- sziku69: Fűzzük össze a szavakat :)
- Luck Dragon: Asszociációs játék. :)
- További aktív témák...
- ASUS ROG Strix GeForce RTX 4070 Ti OC 12GB GDDR6X 192bit Videokártya
- RX570-es, RX580-as és RX5500XT eladó videó-kártyák - Garancia
- Canon EOS 1300D gép szettek, objektívekkel, kiegészítőkkel (1400 - 7900 expos gépek, újszerűek! )
- Macbook Air M2 8/256 100% akku
- Iphone 14 Pro fehér-ezüst 128GB nagyon szép
- Bomba ár! HP ZBook Studio G5 - i9-9980H I 32GB I 1TSSD I Nvidia I 15,6" FHD I Cam I W11 I Gar
- LG 55C4 - 48" OLED evo - 4K 144Hz - 0.1ms - NVIDIA G-Sync - FreeSync - HDMI 2.1 - A9 Gen7 CPU
- ÁRGARANCIA! Épített KomPhone Ryzen 7 5700X 32/64GB RAM RTX 5060Ti 8GB GAMER PC termékbeszámítással
- Bomba ár! HP ZBook FireFly G8 - i7 I 16GB I 512SSD I 15,6" FHD Touch I Nvidia 4GB I Cam I W11 I Gar!
- Lenovo ThinkPad L16 Gen 1 - 16" WUXGA IPS - Ultra 5 135U - 16GB - 512GB - Win11 - 2,5 év gari
Állásajánlatok
Cég: CAMERA-PRO Hungary Kft
Város: Budapest
Cég: Promenade Publishing House Kft.
Város: Budapest