- Mindenki Z Fold7-et akar
- One mobilszolgáltatások
- Kirakatba tette a Google a Pixel 10-eket
- Itt egy pár fotó az iPhone 17 sorozatról
- Profi stratégiára vált a Galaxy S26
- Huawei Mate 9 - Mate evangéliuma
- Samsung Galaxy A56 - megbízható középszerűség
- Kikristályosodik a Razr 60
- Bemutatkozott a Poco X7 és X7 Pro
- Huawei Watch Fit 3 - zöldalma
Hirdetés
Talpon vagyunk, köszönjük a sok biztatást! Ha segíteni szeretnél, boldogan ajánljuk Előfizetéseinket!
Új hozzászólás Aktív témák
-
#2937
Jester01
veterán
PindurAnna
#2936
Jester01
veterán
válasz
PindurAnna
#2936
üzenetére
Hát miért nem vettél neki építőkockákat
Na, építsünk tornyokat. Minden magasságnál tartsuk nyilván hány olyan van aminek piros a teteje és hány aminek fehér. Amikor a következő emeletet ráhúzzuk, akkor pirosat bármilyenre tehetünk de fehéret csak pirosra. Tehát ha P, F az előző és P', F' az új emelet, akkor P'=P+F és F'=P.
Mindenki kicsiben kezdi, nézzük az 1 emeletes tornyokat. Nyilván 1 piros tetejű és 1 fehér tetejű a választék, ezt (1,1) formában írom. Innentől már csak a fentebb megállapított szabályt kell alkalmazni (Rózsa György-féle "Kapcsoltam" stílusban: ez első számból lesz a második, az új első pedig a két régi összege):
1: (1,1)
2: (2,1)
3: (3,2)
4: (5,3)
5: (8,5)
6: (13,8)
7: (21,13)
8: (34,21)
9: (55,34)
10: (89,55)Tehát 10 emeletesből van 89 aminek piros a teteje és 55 aminek fehér, ez összesen 144.
-
Jester01
veterán
A második egyenlet alapján (T1-T2)-t helyettesítették az elsőbe, mi a probléma?
(1/2)*m*R*a = R (g(m1 - m2) - a(m1 + m2)) - M = Rg(m1-m2) - Ra(m1 + m2) - M
(1/2)mRa + (m1+m2)Ra = Rg(m1-m2) - M
(1/2)ma + (m1+m2)a=g(m1-m2) - M/R
(m/2 + m1 + m2)a=g(m1-m2) - M/R
a = (g(m1-m2) - M / R) / (m/2 + m1 + m2) -
Jester01
veterán
válasz
zuzu000
#2921
üzenetére
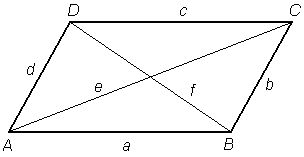
Ugye a paralelogramma átlói felezik egymást, mivel a szembenlévő AOB és COD háromszögek egybevágóak (O a metszéspont). Ha ezen felül még merőlegesek is, akkor mind a 4 O csúcsú háromszög egybevágó (két oldal és a közrezárt szög azonos). Ha pedig egybevágóak akkor értelemszerűen a paralelogramma minden oldala egyforma hosszú és ezért rombusz.
-
#2920
Jester01
veterán
Bjørgersson
#2919
Jester01
veterán
válasz
Bjørgersson
#2919
üzenetére
Nem
, egy matematikus biztos talált volna egyszerűbb megoldást.Egyébként tessék vigyázni, mert az egyik sort érdekesen nem törte el a fórummotor, úgyhogy íme mégegyszer:
r = TAPQ / (AP + PQ / 2) =
= (5/18 * a^2) / (gyök(13)/3 * a + gyök(2) / 6 * a) =
= 5/18 / (gyök(13)/3 + gyök(2) / 6) * a =
= 5 / (6gyök(13) + 3gyök(2)) * a ~ 0.19a. -
Jester01
veterán
válasz
zuzu000
#2917
üzenetére
Szép feladat
Lásd a mellékelt ábrát:
A négyzet oldala legyen a.
Nézzük először az ABP háromszöget. A feladat szerint ennek a területe harmada a négyzetének, vagyis a*BP / 2 = a*a / 3, innen BP=2a/3. Ugyanígy DQ is, az AQD háromszögből, továbbá PC=CQ=a/3. PBE hasonló PCQ-hoz, tehát BE=BP=2a/3. ABS hasonló AEP-hez, vagyis AS / SP = AB / BE = a / (2a/3) = 3 / 2. Tehát az átló a szakaszokat 3 : 2 arányban osztja.A második részben az ASR háromszögbe beírt kör területe kellene. Ehhez előbb nézzük az APQ hasonló háromszöget, majd később arányosítjuk. Ismert képlet alapján a háromszög területe TAPQ=r * s = r * (AP + AQ + PQ) / 2 = r * (AP + PQ / 2), ahol r a beírt kör sugara, s pedig a fél kerület. Pitagorasz képlettel AP = gyök(a^2 + BP^2) = gyök(a^2 + 4a^2/9) = gyök(13)/3*a. PQ pedig gyök(2)/3*a. Továbbá TAPQ=TAPCQ - TPCQ=a^2/3 - a^2/18 = 5/18 * a^2. A beírt kör sugara tehát r = TAPQ / (AP + PQ / 2) = (5/18 * a^2) / (gyök(13)/3 * a + gyök(2) / 6 * a) = 5/18 / (gyök(13)/3 + gyök(2) / 6) * a = 5 / (6gyök(13) + 3gyök(2)) * a ~ 0.19a. Az ASR háromszög ugye 3/5 arányban kisebb, így a beírt kör sugara is, ami így kb. 0.11a. A kör területe a sugár négyzetével arányos, a négyzetbe pedig a/2 sugarú kör fér. Innen a kért arány már adódik, nagyjából (a^2/4) / (0.11a)^2 ~ 20 : 1, a pontos számítást az olvasóra bízom
![;]](//cdn.rios.hu/dl/s/v1.gif)
-
#2913
Jester01
veterán
Apollo17hu
#2912
Jester01
veterán
válasz
Apollo17hu
#2912
üzenetére
Mondjuk nem tudom miért javasolt, szerintem sokkal egyszerűbb kiszorozni/egyszerűsíteni.
Ha a hatványozást/gyökvonást írnák, akkor még érteném. -
#2901
Jester01
veterán
blackvinyl
#2900
Jester01
veterán
válasz
blackvinyl
#2900
üzenetére
Az oldalban a hiba megtalálása meg biztos az informatika feladatsor része
Egyébként az eredmény tényleg –2,2 és el is fogadja, csak a mínusz jel az nem a szokásos hanem az unicode 2013 EN DASH. Másolj ki egy mínusz jelet a kérdésből, azzal jó lesz. -
Jester01
veterán
válasz
ngabor2
#2890
üzenetére
3 van. A szabályos háromszög területe nem 1, tehát a következő 2 lehetőség van:
1) ha a "magányos" oldal a 2cm, akkor a harmadik csúcs az oldalfelező merőlegesen van, mégpedig 1cm távolságban, a T=am/2 miatt. Eddig tehát egy van.
2) ha az egyenlő szárak 2cm-esek, akkor vegyük az egyiket alapnak. A harmadik csúcs az egyik végpont körüli 2cm-es sugarú körön lesz, a háromszög magassága továbbra is 1cm, tehát az olyan távolsában lévő párhuzamos egyenesen is rajta lesz. Ez két metszéspontot ad, egy tompaszögű és egy hegyesszögű háromszöget amik nem egybevágóak. Ez lesz a másik két megoldás, összesen tehát 3.Mind a két eset lehetne a másik irányba is, de azok a háromszögek egybevágóak a fentiekkel.
Az oldalak (2, gyök2, gyök2), (2, 2, 2*gyök(2+gyök3)), (2, 2, 2*gyök(2-gyök3))
Ez egyébként a Heron képletből is minden bizonnyal kijönne. -
-
#2845
Jester01
veterán
Dark Archon
#2844
Jester01
veterán
válasz
Dark Archon
#2844
üzenetére
Rögtön az első lépésnél mit csináltál? Nézem, nézem, de nem értem
Ebből:
Um2*Rg+Um2*RvII = (Um1(Rg+RvI)/RvI)*RvII
Hogy lett ez:
Um2*Rg*RvII+Um2*RvII*RvI = Um1*Rg*RvII+Um1*Rg*RvIAz első jobb oldalán mindenképp van egy Um1*RvII tag, aminek nyoma sincs a másodikban.
-
#2843
Jester01
veterán
Dark Archon
#2842
Jester01
veterán
válasz
Dark Archon
#2842
üzenetére
Mondjuk az elsőből kifejezed Ug-t:
Ug = Um1 * (Rg + RvI) / RvIA másodikat felszorozzuk, hogy egyszerűsödjön és behelyettesítjük Ug-t:
Um2 * Rg + Um2 * RvII = Ug * RvII = Um1 * RvII / RvI * (Rg + RvI) = Um1 * RvII / RvI * Rg + Um1 * RvIIRg tagokat balra:
(Um2 - Um1 * RvII / RvI) * Rg = (Um1 - Um2) * RvIISzorozzunk RvI-el:
(Um2 * RvI - Um1 * RvII) * Rg = (Um1 - Um2) * RvI * RvIIOsztás után:
Rg = RvI * RvII * (Um1 - Um2) / (Um2 * RvI - Um1 * RvII)Hacsak el nem rontottam
-
Jester01
veterán
Az minden bizonnyal 4 bites kettes komplemens számábrázolás. Ott a -3 bizony 1101. Mivel -3=0-3 ezért ki is számolhatod:
0000
-0011
====
1101Illetve a "hagyományos" számítási mód, -x=~x + 1 (vagyis minden bitet negálj majd adj hozzá egyet). Így is kijön:
3=0011, negálva (egyes komplemens) 1100, +1 = 1101 (kettes komplemens) -
Jester01
veterán
A másik háromszöget kell nézni, ami lefelé van, a Föld közepe az egyik csúcsa. Így az egyik oldal a Föld sugara, a másik a műhold pálya magassága. A harmadik innen már Pitagorasz tétellel adódik.
* Persze a te háromszöged is lehet ez, az a lényeg hogy B a Föld középpontja, C a vevő, A pedig a műhold a horizonton. h a pálya magasság, a pedig a Föld sugara.
** és ahol a műhold pálya magasságáról beszélek az nyilván a Föld középpontjától értendő, vagyis a Föld sugár plusz a felszín feletti magasság.
-
Jester01
veterán
Feltételezem az / jel után az egész a nevező, vagyis:
1/(x+5) + 2/(x^2-10x+25) = -10/(x^2-25)
Kis átalakítással:
1/(x+5) + 2((x-5)(x-5)) = -10/((x+5)(x-5))(Itt megjegyezzük, hogy x nem lehet 5 vagy -5)
Felszorozva (x+5)(x-5)(x-5)-el:
(x-5)(x-5) + 2(x+5) = -10(x-5)
x^2-10x+25 + 2x + 10 = -10x + 50
x^2+2x-15=0
(x-5)(x-3)=0vagyis x=5 illetve x=3, de ugye x nem lehet 5, tehát csak x=3.
-
#2767
Jester01
veterán
PindurAnna
#2766
Jester01
veterán
válasz
PindurAnna
#2766
üzenetére
Ha 8 elf nem kósza és az elfek fele kósza akkor összesen 16 elf van.
Minden íjász kósza, és a kószák harmada íjász, és kósza 90 van. Tehát 30 íjász.
Maradt 60 kósza nem íjász. Ezek között már nincs az 1 íjász elf (aki ugye kósza) és a 8 nem kósza elf, tehát van még 7 elf. A maradék pedig a kérdéses nem íjász kósza félelfek, akik tehát 53-an vannak. -
#2759
Jester01
veterán
Dark Archon
#2758
Jester01
veterán
válasz
Dark Archon
#2758
üzenetére
Én meg jól megmondtam, hogy ügyelj a koordináta negyedre és erre én nem ügyeltem arra a fránya mínusz jelre. Szóval a szöghöz PI-t hozzá kell adni (vagy kivonni, mindegy).
-
#2757
Jester01
veterán
Dark Archon
#2756
Jester01
veterán
válasz
Dark Archon
#2756
üzenetére
Ott ülsz a gép előtt és nem tudtad megkeresni?
a+bi => r(cos fi + i sin fi) => r*e^(i*fi), r=gyök(a^b+b^2) (Pitagorasz) tg fi = b/a (koordináta negyedre és nullákra ügyelni)
A a te példádban r~1.5634 fi~1.3823 -
Jester01
veterán
-
Jester01
veterán
-
#2694
Jester01
veterán
PindurAnna
#2693
Jester01
veterán
válasz
PindurAnna
#2693
üzenetére
Ja, az énekeses. Afölött valahogy átsiklottam.
Van 3 Schulze. Tegyük fel, hogy egyik sem Waldemar. Akkor viszont mind a két Meier testvér Waldemar, ami nem lehet. Tehát legalább az egyik Schulze Waldemar.
-
#2692
Jester01
veterán
PindurAnna
#2690
Jester01
veterán
válasz
PindurAnna
#2690
üzenetére
6. Vegyük a bal felső - jobb alsó átlót. Ez 4 lehetőség. A másik átlóból mindegyikhez választhatunk még 2 lehetőség közül. Ezután az első sorban még mindig 2 lehetőség van, de utána már a maradék 2 számnak fix lesz a helye. Így tehát 4*2*2=16 lehetőség van összesen.
-
#2691
Jester01
veterán
PindurAnna
#2690
Jester01
veterán
válasz
PindurAnna
#2690
üzenetére
Te aztán nem apróztad el
1. Mindegyik pont jó kör középpontnak, ez tehát 7. A hatszög középpontját minden oldalra tükrözve is jó, ez tehát újabb 6. Összesen szerintem tehát 13.
2. Ilyesmiben nem vagyok jó mert mindig olyat látok az ábrán ami nem igaz. De talán hasonló háromszögekből 24/18 = x/20
3. ugye (e,f)=(-a, -b) úgyhogy a*b-(-a)*(-b) = 0
4. Legyen a tartály t tömegű és a teljes tejmennyiség x. Akkor:
t + x/2 = 22
t + x/3 = 16
Innen a megoldás már triviális.5. 72=8*9 Mikor lesz osztható a szorzat? Ha 8al és 9el is osztható. 8al akkor lesz, ha 8 vagy többszöröse szerepel, vagy 4 többszöröse és egy páros szám, vagy 3 páros szám. 9el akkor ha 9 vagy többszöröse, vagy két 3 többszöröse. Össze kell számolgatni és kivonni az összes lehetőségből.
6. na ehhez már most nincs erőm
-
Jester01
veterán
válasz
PazsitZ
#2688
üzenetére
A másodikra nekem sincs jó ötletem, de ha nem rontottam el a programot meg a téglalapokat akkor 144 a megoldás.
Indulásnak már az bezavar, hogy nem bármelyik 4 pontot kell ellenőrizni, csak azokat, amikből téglalap lesz. Én 10 téglalapot számoltam össze. Ezután gondoltam a teljes 2^9 lehetőségből kivonogatom a rosszakat, de az átfedések miatt ebből csak fejfájás lett, nem eredmény
... egyelőre. Hetedikes feladatnak nagyon durvának tűnik. -
Jester01
veterán
válasz
fpeter07
#2682
üzenetére
Nem tudom pontosan melyik képletet, illetve milyen kiindulási alapból.
Például az irányvektoros egyenletből a távolság(négyzet) képletének deriválásával le lehet valamit vezetni. Célszerű egyenes és az origó távolságát venni, az általános eset eltolással innen már kijön. -
#2667
Jester01
veterán
korpicschess
#2666
Jester01
veterán
válasz
korpicschess
#2666
üzenetére
És vajon miért
-
Jester01
veterán
1.
átalakítod először tízesbe, összeadod, majd visszaalakítod
-vagy-
eleve nyolcasban végzed el az összeadást.Mi okozza a problémát?
2. ezt majd később
3. prímtényezőkre bontod aztán kombinatorika
4. 6-al akkor osztható, ha 2-vel és 3-al is. 2-vel akkor ha páros vagyis az utolsó számjegye 2-vel osztható. 3-al akkor, ha a számjegyek összege osztható 3-al. Vagyis, fogod az összes páros számjegyet és bepróbálod y helyére, megnézve mik adódnak x-re. -
#2661
Jester01
veterán
superecneB
#2660
Jester01
veterán
válasz
superecneB
#2660
üzenetére
Akkor szerintem jó
-
#2659
Jester01
veterán
superecneB
#2658
Jester01
veterán
válasz
superecneB
#2658
üzenetére
Az x kimaradt az elsőből, és ha jó sejtem adtak peremfeltételt, hogy y(0)=1 és kérdezték az y(1)-et?
-
#2657
Jester01
veterán
superecneB
#2655
Jester01
veterán
válasz
superecneB
#2655
üzenetére
Ilyet már nagyon rég csináltam, tehát lehet, hogy ez nem jó (bár visszaellenőrizve nekem kijön):
dy/dx = 3x^2*y
1/y dy = 3x^2 dxintegrálva:
ln y = x^3+C
y = e ^ (x^3 + C) -
#2649
Jester01
veterán
PindurAnna
#2647
Jester01
veterán
válasz
PindurAnna
#2647
üzenetére
Az első helyen nem lehet nulla, a maradék 3 bármelyike lehet.
{nem 0, 0, bármi, bármi} + {nem 0, nem 0, 0, bármi} + {nem 0, nem 0, nem 0, 0}) = 9*1*10*10 + 9*9*1*10 + 9*9*9*1 = 2439
MOD: kibontottam
-
#2646
Jester01
veterán
PindurAnna
#2645
Jester01
veterán
válasz
PindurAnna
#2645
üzenetére
Azért mert távolságra kell számolni nem időre. Ha ugyanannyi ideig ment volna a kétféle sebességgel, akkor lehetne középértékkel számolni. Mivel viszont itt a távolság volt fix, ezért a második kör tovább tartott, vagyis több ideig ment lassabban így az átlagsebesség alacsonyabb a középértéknél.
Képlettel, ha l a kör hossza:
v = s / t = 2l / (t1 + t2) = 2l / (l/v1 + l/v2) = 2 / (1/v1 + 1/v2) = 144 -
#2643
Jester01
veterán
róbert gida
#2639
Jester01
veterán
válasz
róbert gida
#2639
üzenetére
1. (Tessék rajzolni!) Egyenlő szárú hárömszög megfelelő magasságvonala szögfelező és szimmetriatengely, tehát van egy derékszögű háromszögünk melynek a területe fele az eredeti háromszögnek és oldalai a, c/2, m. Szinusz, koszinusz definícióból c/2=a*sin(gamma/2) és m=a*cos(gamma/2), a terület pedig T/2=m/2*c/2 behelyettesítve gamma adódik. Utána mivel alfa=béta és a háromszög szögeinek összege 180, a másik két szög is megvan.
A köréírt kör esetén két oldalfelező merőlegessel ismét derékszögű háromszög van, innen r=a/(2 * cos(gamma/2))
Beírt kör esetén két szögfelezővel van derékszögű háromszög, innen r=tg(alfa/2)*c/2
A kör sugarakra vannak közismert képletek is, ha nem szükséges levezetni.
2. Ehhez igazából csak a kör területképletét kell ismerni, azt meg remélem egy gimis lány már tudja használni.
-
Jester01
veterán
3. erre biztos van egyszerűbb megoldás is, de nekem csak ez a megszámolósdi jutott az eszembe:
1*8 = 1
2*1 1*6 0*1 = 7 * 7
2*2 1*4 0*2 = 21 * 15
2*3 1*2 0*3 = 35 * 10
2*4 0*4 = 35
3*1 1*5 0*2 = 21 * 6
3*1 2*1 1*3 0*3 = 35 * 5 * 4
3*1 2*2 1*1 0*4 = 35 * 4 * 3
3*2 1*2 0*4 = 35 * 6
3*2 2*1 0*5 = 21 * 3
4*1 1*4 0*3 = 35 * 5
4*1 2*1 1*2 0*4 = 35 * 4 * 3
4*1 2*2 0*5 = 21 * 3
4*1 3*1 1*1 0*5 = 21 * 3 * 2
4*2 0*6 = 7
5*1 1*3 0*4 = 35 * 4
5*1 2*1 1*1 0*5 = 21 * 3 * 2
5*1 3*1 0*6 = 7 * 2
6*1 1*2 0*5 = 21 * 3
6*1 2*1 0*6 = 7 * 2
7*1 1*1 0*6 = 7 * 2
8*1 0*7 = 1
összesen = 3432A táblázat azt mutatja, adott számjegyből hány darab van. Például a második sor 2*1 1*6 0*1 az az eset, amikor 1db 2-es, 6db 1-es és 1db 0-ás számjegy van. A lehetőségeket simán (n k) kombinációval számoltam, a tagokat összeszorozva és ügyelve arra, hogy 0 nem lehet a szám elején (mert akkor csak 7 jegyű lenne).
-
#2637
Jester01
veterán
Dr. Student
#2636
Jester01
veterán
válasz
Dr. Student
#2636
üzenetére
A szimbolikus a képletet adja meg, a numerikus egy adott pontra közelítő módszerekkel kiszámolja neked.
Például az x^2 deriváltja 2x szimbolikusan, numerikusan viszont csak olyat tud mondani, hogy az x=0.5 pontban a derivált értéke 1. Ez a leírás alapján valahogy így nézhet ki: d/dx( x^2, 0.5 ) erre ki kellene adnia, hogy 1.
-
Jester01
veterán
Melyik részét nem érted?
Adott ez: 10A+B = K(A+B)
Rendezd át úgy, hogy vagy az A-t vagy a B-t (tetszés szerint) kifejezed belőle. Tehát valami olyan forma legyen, hogy A=X ahol X-ben már nincs A csak B és K.
Ezután ezt szépen be kell helyettesíteni a másik hányadosba, vagyis ami eddig az volt, hogy (10B+A)/(A+B) abból most az lesz, hogy (10B+X)/(X+B), így az A egyből eltűnik. A törtet egyszerűsítve meglátod, hogy a B is kiesik és csak a 11-K marad. -
Jester01
veterán
1) Mivel a legkisebb számjegy 2 a legnagyobb pedig 6, így biztos, hogy az eredeti szám 4 jegyű volt. Legyen ez ABCD, értéke nyilván 1000A+100B+10C+D, számjegyeinek összege A+B+C+D. A kettőt kivonva K=999A+99B+9C lesz. Vegyük észre, hogy K osztható 9-el, annak a feltétele pedig az, hogy K számjegyeinek összege osztható legyen 9-el. Ez ugye akkor sem változik ha összekeverjük. A feladatban megadott eredmény számjegyeinek összege 2+3+4+5+6=20 ami 9-el osztva 2 maradékot ad, vagyis egy ilyen számjegyet kell elvenni ez pedig csak a 2-es lehet.
2) Legyen a szám AB akkor az értéke 10A+B, számjegyeinek összege A+B, a feladat szerint 10A+B = K(A+B). A megfordított szám BA, értéke 10B+A számjegyeinek összege ugyanúgy A+B persze. Keressük a (10B+A)/(A+B) hányadost. Egyszerűen fejezzük ki az ismert 10A+B = K(A+B) egyenletből A-t vagy B-t a másikkal, majd tegyük bele a keresett képletbe. Némi átalakítás után a hányados értékére 11-K adódik. Példa: 63=7*9, K=7. Fordítva 36=4*9 és valóban 11-7=4.
-
#2630
Jester01
veterán
Dr. Student
#2628
Jester01
veterán
válasz
Dr. Student
#2628
üzenetére
Fogod a leírást és fellapozod a megfelelő oldalon?
d/dx( f(x), a, tol )
f(x): Function of X (All non-X variables are treated as
constants.)
a: Input a value to specify the point for which the derivative
should be obtained (differential point)
tol: Tolerance range (input/output format: Linear)
You can omit specification of the tolerance range. A default value
of 1 × 10^-10 is used when you do.Igen, ez is numerikus persze.
-
Jester01
veterán
Csak te azt mondtad, hogy a 108 az már az elforgatások nélkül van, az enyémekben viszont azok még benne vannak. Ha jól látom a 39. és az 52. az elforgatásra invariáns, a maradék 88 pedig valószínűleg mind a 4 verzióban megvan. Tehát azokat kiszűrve marad 22 + 2 = 24.
De ez még mindig nem levezetés
-
Jester01
veterán
válasz
cellpeti
#2581
üzenetére
Ha a számlálót és a nevezőt ugyanazzal a számmal szorzod akkor nyilván nem változik a tört értéke. Jelen esetben 2-vel szorzott, a nevezőben pedig bevitte a gyök illetve a négyzetek alá.
(x / y) = 1 * (x / y) = (2 / 2) * (x / y) = (2 * x) / (2 * y)
továbbá
y * gyök(x) = gyök(y^2 * x)
és
y * (x^2) = (gyök(y) * x) ^ 2
valamint
z * (x + y) = (z * x) + (z * y) -
Jester01
veterán
válasz
Jhonny06
#2574
üzenetére
Ez a lépés nem használta még a bizonyítandó egyenlőtlenséget. Pontosan annyi történt, ami oda van írva, vagyis alkalmazták az előző tételt a b és a-b számokra.
Hogy a változókkal kisebb kavarodás legyen, vegyük az előző egyenlőtlenséget x és y változókkal:
|x| + |y| >= |x + y|
Itt végeztek x=b és y=a-b helyettesítést, amivel egyszerűen adódik az ami a képen is van:
|b| + |a-b| >= |b + (a-b)| = |a|
-
Jester01
veterán
ha kifejezzuk az y -t ennél a példánál maradt egy tiszta szám ismeretlen nélkul
Nem tudom melyik példáról beszélsz mert a fentiekben nincs ilyen. De ha valaha ilyen kijön, akkor az egy vízszintes egyenest jelent, hiszen az y akkor állandó.
Az x 0 ,ez tetszőlegessen adjuk meg mink és áltb. 0 át szoktak?
Igen. Az egyeneshez két pont kell, vagy egy pont és a meredekség. Az ax+b formájú egyenletbe x=0 helyettesítése egyszerű, hiszen ilyenkor csak a b marad. De bármilyen x-et helyettesíthetsz mivel az egyenlet bármilyen x-re megmondja az y-t.
az A rész a meredekségi szog,ami lehet tort,ismeretlenes szám
ax+b egyenletben az a-ban már nincs ismeretlen, az egy szám. Azt mutatja meg, egységnyi x-re mennyi y változás jut. Ha 3/2 akkor azt vagy úgy mondod, hogy egységnyi x-re 3/2 y jut, vagy 2 x-re 3 y. (felszoroztam kettővel). Rajzolásnál tehát vagy 1-et mész jobbra és 3/2-et le, vagy 2-t mész jobbra és 3-at le. Nézd meg, ez a kettő ugyanolyan meredek, csak az egész számokat könnyebb rajzolni.
-
Jester01
veterán
Előbb a 2. pont és aztán az 1.
Vegyük a (-3/2)x + 7 egyenest. Nézzük mi lesz x=0 esetén: 7. Szóval az egyik pont 0,7 (vagyis 7-nél metszi az y tengelyt). A -3/2 a meredekség ahogy mondtad. Ha negatív akkor lefelé megy, ha pozitív akkor felfelé. Ez tehát lefelé megy, mégpedig minden 2 lépésre 3-at. Ez alapján meg tudod már rajzolni.
Hasonlóan a másik egyenes: (-1/4)x + 2. Ez 2 magasan metszi az y tengelyt és minden 4 lépésre 1-et megy le.
Most jön az 1. pont, miszerint megkeresed a metszéspontot és egyszerűen leolvasod. Innen jön ki az x=4 y=1
Végül jön az ellenőrzés.
-
Jester01
veterán
Mármint, hogy egy egyenest hogyan kell ábrázolni? Például fogsz két tetszőleges pontot róla és összekötöd. Általában az x=0 kényelmes, az rögtön az egyik tengelymetszet lesz. Ezen felül meg választhatsz egy másikat. Avagy, az x=0 pont után az egyenes meredekségét felhasználva rajzolod meg. Ez ugye az x tényező szorzója, jelen esetben 2, tehát egyet jobbra kettőt fel.
-
#2533
Jester01
veterán
MasterDeeJay
#2532
Jester01
veterán
válasz
MasterDeeJay
#2532
üzenetére
Vegyük hozzá a 4 pixelnyi margót a négyzetekhez, ezzel minden négyzet 68x68 helyet foglal, így:
A(i, j) = (68 * i, 68 * j) + (50, 50)
C(i, j) = A(i, j) + (64, 64)
Ha i,j az oszlop illetve sor nullától számolva. -
Jester01
veterán
válasz
Gyuker0
#1574
üzenetére
Ezekhez csak egy ábra kell, mégpedig egy derékszögű háromszög. Azontúl pedig a sin/cos/tg definíciók alapján egyszerűen adódik az eredmény. Pl. az első feladat: adott a szög és az átfogó, keressük a szemközti oldalt. Melyik az a szögfüggvény amiben ezek szerepelnek? Hát a szinusz: sin a = szemközti / átfogó. Ebből kettőt ismersz tehát a harmadik kiszámítása nem lehet gond.
-
-
#1381
Jester01
veterán
concret_hp
#1380
Jester01
veterán
válasz
concret_hp
#1380
üzenetére
Nehéz eldönteni, hogy hülyéskedsz vagy nem
-
Jester01
veterán
válasz
sagesz93
#1345
üzenetére
Azok négyzetszámok lesznek
És ha ismered a szorzótáblát, akkor nem okozhat gondot a lista előállítása 1*1=1, 2*2=4, 3*3=9, 4*4=16, 5*5=25, stb.
Amikor a gyök alá beviszed akkor kell szorozni önmagával (ez a négyzetre emelés). Ha kiveszed akkor nem osztani kell, hanem gyököt vonni.
6*gyök(valami) = gyök(36 * valami)meg vagyok döbbenve, hogy ezt 10.-ben tanítják ...
-
Jester01
veterán
Hát én ugye a brute-force megoldást implementáltam, ennek megfelelően a pontok koordinátáit vittem fel és a köztük lévő éleket. Nekem a koordináták azért kellettek, hogy meg tudjam állapítani minden pont valóban csúcs-e illetve bizonyos élek nem metszik-e egymást.
*Ja a bevitelhez lehet egy rajzolóprogram-szerű felületet csinálni.@concret_hp: az enyém elvileg bárhány oldalú sokszögre megy
-
#1214
Jester01
veterán
concret_hp
#1213
Jester01
veterán
válasz
concret_hp
#1213
üzenetére
Na megcsináltam az atom brute-force megoldást, a háromszöges az stimmel, de a négyszőges az 82 lesz. Szúrópróba-szerűen ellenőriztem egy párat, eddig nem találtam hibát. Lehet, hogy nem négyszöget kell keresni, hanem azon is háromszöget? Mert abból valóban 30at találtam.
-
Jester01
veterán
Simán a fekete szakasz szögét kiszámolod majd ez alapján a piros vektorokat legyártod elforgatással és szépen hozzáadod a kívánt végponthoz.
Kb így:
adott: P0(x0, y0), P1(x1, y1), r és alfa
szakasz szöge beta = atan2(y1 -y0, x1 - x0)
nyíl szögek gamma0 = beta + alfa, gamma1 = beta - alfa
elforgatott hegy Q0(x2, y2) = (r * cos(gamma0), r * sin(gamma0))
Q1(x3, y3) = (r * cos(gamma1, r * sin(gamma1))
eltolt nyílhegyek végpontja:
R0 = P1 - Q0 = (x1 - x2, y1 - y2)
R1 = P1 - Q1 = (x1 - x3, y1 - y3)Kész. Annyi trükk van benne, hogy beta számolásnál figyelni kell a helyes koordináta negyedre (ezért használtam atan2-t) illetve a piros szakaszok helyett azok ellentettjét könnyebb számolni ezért a kivonás a végén.
Itt egy példakód C#-ban:private Gdk.Point GetHalfArrow(Gdk.Point P1, double gamma, int r)
{
Gdk.Point Q = new Gdk.Point((int)(r * Math.Cos(gamma)), (int)(r * Math.Sin(gamma)));
Gdk.Point R = new Gdk.Point(P1.X - Q.X, P1.Y - Q.Y);
return R;
}
private void DrawArrow(Gdk.Point P0, Gdk.Point P1, int r, double alpha)
{
double beta = Math.Atan2(P1.Y - P0.Y, P1.X - P0.X);
Gdk.Point R0 = GetHalfArrow(P1, beta + alpha, r);
Gdk.Point R1 = GetHalfArrow(P1, beta - alpha, r);
// draw 3 lines: P0-P1 for body, P1-R0 and P1-R1 for the head
} -
Jester01
veterán
Azt tudom, 14!
Mivel megmondtad, hogy kis Fermat, tehát én ezt csináltam:
100^64 = (100^32)^2 = (10000 * 100^30) ^ 2 = (*)
Ide most jól bedugom a kis Fermat-ot:
(*) = (10000 * (31k + 1))^2 = (310000k + 10000) ^ 2 =
(310000k)^2 + 2 * 3100000000k + 100000000Mivel az első két tényező világosan látszik, hogy 62 többszöröse (le is oszthattam volna, de ahhoz most lusta vagyok), így ennek a maradékát 62-vel osztás után csak a 100000000 tag adja. Azt meg talán ki szabad már számolni.
MOD: lemaradt néhány nulla
-
Jester01
veterán
Írjuk fel a keresett számot 3 * 10^n + x alakban (x<10^n pozitív egész)
Ekkor:
3*10^n+x = 3 * (10 * x + 3)
3*10^n+x = 30*x + 9
3*10^n = 29*x + 9
3*10^n - 9 = 29*x
Namost ide kellene valami okosság, ami nekem nem volt, tehát favágó módszerrel elindultam:
n = 27 => 3103448275862068965517241379
n = 55 => 31034482758620689655172413793103448275862068965517241379
n = 83 => 310344827586206896551724137931034482758620689655172413793103448275862068965517241379
Innen az a sejtésem, hogy a 3103448275862068965517241379 sorozat tetszőleges számú egymás után írása jó megoldás, de ugyanakkor még más megoldás is lehet.
Erről mindenesetre ránézésre látszik, hogy az első számjegye 3, a szám maga 3-al osztható, és az utolsó számjegye ilyenkor 3 lesz. Eddig tehát rendben
Innen talán teljes indukcióval már bizonyítható.
Van jobb ötlete valakinek? -
#739
Jester01
veterán
-=Lord Tom=-
#738
Jester01
veterán
válasz
-=Lord Tom=-
#738
üzenetére
Az mínusz, nem?
Abszolútértéket ha jól emlékszem úgy bontunk fel, hogy vizsgáljuk a pozitív meg a negatív esetet.
Vagyis pl. a külső abszolút értéket felbontva:
1) ha |x| - 1 >= 0, akkor |x| - 1 = 4 + x
2) ha |x| - 1 < 0, akkor 1 - |x| = 4 + x
Ugyanez mégegyszer:
1A) ha |x| - 1 >= 0 és x >= 0, akkor x - 1 = 4 + x => -1 = 4, nincs m.o.
1B) ha |x| - 1 >= 0 és x < 0, akkor -x - 1 = 4 + x
2A) ha |x| - 1 < 0 és x >= 0, akkor 1 - x = 4 + x
2B) ha |x| - 1 < 0 és x < 0, akkor 1 + x = 4 + x => 1= 4, nincs m.o.
1B) ha x <= -1, akkor -2x = 5 => x = -2,5
2A) ha 0 <= x < 1, akkor -3 = 2x => x = -1,5 lenne, de nem teljesíti a feltételt.
Tehát a megoldás csakis az x = -2,5. Szvsz.
MOD: jav
[Szerkesztve] -
Jester01
veterán
-
Jester01
veterán
1. Vegyük észre, hogy valós számokra nem lehet egynél nagyobb a szorzat, és egy is csak akkor ha a tagok külön-külön is egy abszolút értékûek, mégpedig vagy mind pozitív vagy 2 negatív.
2. def szerint tg^2 = sin^2/cos^2 valamint legyen y = 2x. Ezzel:
(sin^2(y) - 1)/(cos^2(y)) < 1
Továbbá cos^2 + sin^2 = 1, vagyis:
-1 < 1, ez pedig mindig igaz (de figyelembe kell venni az eredeti egyenlõltenség értelmezési tartományát)
3. add össze illetve vond ki a 2 egyenletet, abból összegképlet lesz:
cos(x-y) = 0
cos(x+y) = gyok3/2 -
#544
Jester01
veterán
Forest_roby
#542
Jester01
veterán
válasz
Forest_roby
#542
üzenetére
Esetleg az segíthet, ha az (a+b)(a-b)=a^2 - b^2 képlettel átalakítod:
t^2/(t+1) = ((t^2 - 1) + 1) / (t+1) = (t-1) + 1 / (t+1) -
#526
Jester01
veterán
Forest_roby
#524
Jester01
veterán
válasz
Forest_roby
#524
üzenetére
Ezt nagyon nem értem, ez egy sima a*x + b alakú függvény, mert epszilon1 és 2 valamint d konstansok. a = (1/d)*( 1/epszilon2 - 1/epszilon1 ), b = 1/epszilon1.
A határozatlan integrál nyilván a/2 * x^2 + b * x + C lesz. Szépen behelyettesíted és kiszámolod a határozottat. Mi a probléma? -
Jester01
veterán
A konstansokra rájöttem, a behelyettesítő képnél már úgy számoltam, csak elfelejtettem odaírni
A két metszéspont x=-2 és x=0, vagyis innen is lemaradt egy mínuszjel.
MOD: a komplex számos feladatnál rögtön az elején elrontottad a szög kiszámítását, mert nem vetted figyelembe, hogy melyik negyedbe esik. Szóval helyesen 5 Pi / 4.
[Szerkesztve] -
Jester01
veterán
Akkor gondolom a kisebből akartam a nagyobbat kivonni, és azért lett negatív?
Egyszerûen elrontottad a kivonást, rosszul bontottad fel a zárójelet: (x^2 + 1) - (1 - 4x - x^2) = x^2 + 1 - 1 + 4x + x^2
A terület valóban nem lehet negatív, de az integrál az igen.
Az első derivált oks, csak az egyből úgyis 0 lesz, azért nem írtam oda ... ez meg egy sima mon csökkenő fv
??? Nem. Az elsõ derivált ln x + 1 lesz, ami x < 1/e esetén negatív, itt az eredeti fv csökken, x > 1/e esetén pozitív, itt pedig nõ.
[Szerkesztve] -
Jester01
veterán
Az elsõ feladat: Rosszul rendezted az egyenletet, a konstans tagok kiütik egymást. Egyébként pedig nem tudjuk mi is a feladat de ha a 2 függvény különbségét kell integrálni akkor nem jó, mert rosszul vontad ki õket egymásból. Végezetül pedig az eredmény elõjele sem jó.
A második feladatnál a k=0 esetben valamit elszámoltál, mert az a k=2 eset párja lenne. És a jó esetekben is 1 + i jön ki visszaellenõrzésnél, valahol elbuktad az elõjelet.
A 4. példát azt most nem néztem meg.
A függvény diszkussziónál a második derivált is jó, de csak véletlenül, mert rossz függvénnyel számoltál. Az elsõ derivált ugyanis ln x + 1, mint ahogy azt oda is írtad.
A monotonitáshoz az elsõ derivált elõjelét kell nézni, ezt a mondatodat nem is értem: ''De itt ha jól sejtem, csak 1 van (a 0)''.
x persze, hogy nem lehet negatív, hiszen ott az eredeti függvény sem értelmezett (mellesleg oda is van írva). -
Jester01
veterán
válasz
szandisas
#509
üzenetére
Lehet, hogy nem hajnalban kellene ilyesmin törni a fejed?
Ha meg mégis, akkor olvasd el még párszor lenox hszét, mert az a magyarázat.
Mégegyszer, kicsit másképp: $30 = $25 + $2 + $3. Kiinduláskor van összesen $30 a ''rendszerben'', a végén ebbõl 25 a recepciósnál, 2 a futárnál, 3x1 pedig a 3 vendégnél lesz. És nem hiányzik semmi.
Ez amúgy inkább a logikai feladványok topikba való, lehet, hogy volt is.
[Szerkesztve] -
#505
Jester01
veterán
Forest_roby
#504
Jester01
veterán
válasz
Forest_roby
#504
üzenetére
Veled értek egyet én is, na nem mintha ez bármire garancia lenne
MOD: az lehet, hogy valami fizikai ok miatt késõbb megfordul az elõjel, de az integrálás az így a helyes szerintem.
[Szerkesztve] -
#503
Jester01
veterán
Forest_roby
#502
Jester01
veterán
válasz
Forest_roby
#502
üzenetére
Nem lehet jó, hiszen a konstans szorzó ki van emelve elõre. A függvény tkp ennyi: C * 1/r^2
Ha C negatív, akkor függvény az ábrának megfelelõ. Viszont ebben az esetben definíció szerint az integrál is negatív kellene legyen. Csakhogy nem lesz, mert a zárójeles kifejezés negatív és ugye most C is, a kettõ szorzata így pozitív. -
#500
Jester01
veterán
Forest_roby
#499
Jester01
veterán
válasz
Forest_roby
#499
üzenetére
Most már én nem értem. Az ábrázolt függvény nem az, amit integráltál. Lemaradt egy mínusz jel?
-
#498
Jester01
veterán
Forest_roby
#497
Jester01
veterán
válasz
Forest_roby
#497
üzenetére
Szerintem is rossz, mivel így az integrál értéke negatív lesz. A függvényt ábrázolva pedig világosan látszik, hogy a pozitív a helyes.
, egy matematikus biztos talált volna egyszerűbb megoldást.
![;]](http://cdn.rios.hu/dl/s/v1.gif)
Innen talán teljes indukcióval már bizonyítható.
Új hozzászólás Aktív témák
axioma
- Gigabyte 15 G5 Gamer FHD IPS 144Hz i5-12500H 12mag 4.5Ghz 16GB 512GB Nvidia RTX 3050 Win11 Garancia
- Layer 2 Plus (Layer 3 Lite) Passzív rack switch, 24x1G + 4x10G SFP+ , SFP-kkel FS S3900-24T4S-R
- Eladó/Lenovo X240 Ultrabook/I5-4300U/8GB DDR3/Win 10Pro/12,5"!!!
- LG OLED55C9 prémium TV - 140cm, 4k, 120Hz - apró vizuális hibával
- Erős Gamer / Munka PC i7-14700, RTX 3070 Ti, 32GB RAM, 1TB SSD
- GYÖNYÖRŰ iPhone 13 mini 256GB Pink -1 ÉV GARANCIA - Kártyafüggetlen, MS3061, 96% Akkumulátor
- GYÖNYÖRŰ iPhone 11 Pro 64GB Space Grey -1 ÉV GARANCIA - Kártyafüggetlen, MS2051
- REFURBISHED és ÚJ - HP Thunderbolt Dock G2 230W docking station (3TR87AA)
- AKCIÓ! Apple Macbook Pro 16" 2019 i9 9980HK 64GB DDR4 512GB SSD Radeon Pro 5500M garanciával
- Samsung Galaxy Book2 Pro 360 i7-1260P 16GB 512GB OLED touchscreen, GARANCIA: 1ÉV
Állásajánlatok
Cég: FOTC
Város: Budapest