Hirdetés
- Visszatérnek a Samsung tervezte CPU-magok és GPU az Exynos 2800-ban?
- QWERTY billentyűzetes, üzenet-fókuszú androidos mobil a Clicks Communicator
- Milyen okostelefont vegyek?
- OnePlus 15 - van plusz energia
- Xiaomi 15T Pro - a téma nincs lezárva
- One mobilszolgáltatások
- Félmillió felett a kiszállított Xiaomi autók száma
- Vivo X200 FE – fenséges méret
- Okosóra és okoskiegészítő topik
- Samsung Trifold, Pebble, Bosch, AI, AI, meg AI - CES 0. nap
Új hozzászólás Aktív témák
-

jerry311
nagyúr
Koszonom mindenkinek!

Legalabb megertettem, hogy nem en vagyok teljesen retard a feladathoz.
-

axioma
Topikgazda
válasz
 jerry311
#6680
üzenetére
jerry311
#6680
üzenetére
Ez egy Medve-matek feladat, meghozza abbol is a szoro agban [semmi, ezust, arany a feladatok besorolasa]
Nem standard matekorai feladat, es nem is matektanar feltetlen, aki megalkotta [ismeros pl. volt a szervezocsapatban es kertek otleteket toluk is - rengeteg feladat megy ki evente, sok helyszin, sok kategoria, me'g ha van is atfedes].
A rendezvenyen [direkt nem versenynek mondom, bar az, de a seta/futas sebessege is beleszamolodik] csak a vegeredmenyt kell bemondani. En egy ilyen szituban siman ha talalok 1999-hez pa'rt, akkor beirom. -

VoidXs
nagyúr
Gondolkodtam tovább, csak nem bírok túllenni ezen a feladaton: "ha Zsuszi későbbi évben született volna" - ez semmit nem mond Zsoltiról, mi több, implikálja, hogy Zsolti korát megtartjuk, hiszen a triviális egyenlőséget hozzá példának. Az 1996 - 2014 párra is igaz ez az állítás, mert ha 97, 98, stb-ben született volna, nem lenne egyenlőség, de 2014 és 2014 esetében van. Az állítás tehát ezzel az eredménnyel sem sérül, nincs köztes elfogadható évszám, amennyiben Zsolti fix. Persze, több, mint valószínű, hogy úgy értették, ahogy többen is gondoltátok, de nem ez van odaírva.
-

VoidXs
nagyúr
válasz
 Jester01
#6684
üzenetére
Jester01
#6684
üzenetére
Basszus, tényleg. Én azt úgy értelmeztem, hogy ha előfordulhatott volna olyan, hogy az egyik gyerek ugyanazon évére több másik is lehetséges, akkor azok közül a nagyobb a jó. De mivel ilyen nem fordulhat elő, eleve redundáns infó lenne. Így már valid ötödikes feladat.

Viszont felmerül a kérdés: hogyan látod be ötödikesként, hogy csak konstans 18 különbség lehetséges? Merthogy ehhez kell az általános megoldást ismerned.
-

VoidXs
nagyúr
válasz
 Jester01
#6682
üzenetére
Jester01
#6682
üzenetére
Ha fixálod az egyik évet, egy pillanat alatt kijön a másik. Ha ez egy órai feladat, azt tudom egyedül elképzelni. Ez viszont nem fair, mert tettél egy extra kitételt a feladat mellé.
Ez úgy jó ötödikes feladat, ha mondjuk legalább annyit mondanak, hogy az idősebb 1994-ben született. Ott a helyes megoldás a brute force, hiszen egyetlen megoldás van, maximum azt kell egy kicsit alaposabban bizonyítani, hogy több nem is lehet.
Azt is tegyük hozzá, hogy nem lehet egyértelmű választ adni az eredeti kérdésre, hiszen végtelen megoldás is lehet, abból meg hogy mondod meg, hogy most hány éves biztosan a gyerek?
-

Jester01
veterán
Az brute force, hogy ha már tudod, hogy 2000 után nem jó akkor kipróbálod az 1999-et? (Tekintve, hogy a legnagyobbat keressük)
-

VoidXs
nagyúr
b1 = 9 és b2 = 0, bocsánat. Ekkor először is
11 * c1 + 2 * d1 = 11 * c2 + 2 * d2 + 92,
majd eredmény: c2 = c1 + 2n és d2 = d1 - 11n - 46, n eleme Z, kikötések kellenek, ekkor vegyük észre, hogy n = -4 (mert bármi más lenne, d1 és d2 különbsége > 10, miközben egyjegyűek), ami miatt c2 = c1 - 8 és d2 = d1 - 2,
azaz mondjuk 1996-ra 2014. Mivel mindkét egyenes meredeksége megegyezik, a "gyerekek" korkülönbsége csak és kizárólag konstans lehet, ez a példa esetben 18. Ez más évszázadokkal már nem feltétlenül van így.Nem tudom elképzelni, hogy itt brute force legyen a hivatalos megoldás.
-

VoidXs
nagyúr
válasz
 jerry311
#6673
üzenetére
jerry311
#6673
üzenetére
Első lépésként tegyük fel, hogy valid jelenkori születési évekről van szó, különben az is jó megoldás lenne, hogy Zsolti Kr. u. 8-ban született, Zsuzsi meg 13-ban. Írjuk fel az egyenleteket. Az évszám számjegyeivel dolgozunk, legyenek a, b, c, d, így az évszám:
1000a + 100b + 10c + d.
Fejtsük a feladatot is egyenletbe, először is:
"hozzáadja a születési évszámához" = x + a + b + c + d.
Behelyettesítés és egyszerűsítés után azt kapjuk, hogy
1001a + 101b + 11c + 2d.
Legyen a1, a2, b1, b2, stb. a két testvérre az egyenlet két oldalán:
1001 * a1 + 101 * b1 + 11 * c1 + 2 * d1 =
1001 * a2 + 101 * b2 + 11 * c2 + 2 * d2Itt tudsz egyszerűsíteni azzal, hogy 2 eset lehetséges:
a) a1 = a2, ekkor ezek kiesnek, és igazából dobhatod ki vele a b-ket is, mert 2100-as meg 1800-as gyerek nem lesz, illetve
b) a1 < a2, vagyis a1 = 1 és a2 = 2. Ekkor nyilván b1 = 0 és b2 = 9.Ez az a pont, ahol megfájdult a fejem, mert egészértékű programozással, ami egyetemi tananyag, könnyen kizárod a-t, és b-re is kidobja neked a választ két egyenes formájában, de azt biztos nem tanulta egy ötödikes, és az istenért se jövök rá, hogy mi ennek az egyszerű módja.
-

TDX
tag
válasz
 jerry311
#6673
üzenetére
jerry311
#6673
üzenetére
A legutolsó néhány évtizedben a következőképp alakul a művelet után kapott szám:
202x -> 2024+2x, tehát 2024-2042 közötti páros számot kapunk a művelet elvégzése után
201x -> 2013+2x: 2013-2031 páratlan
200x -> 2002+2x: 2002-2020 páros
199x -> 2009+2x: 2009-2027 páratlan
198x -> 1998+2x: 1998-2016 páros
197x -> 1987+2x: 1987-2005 páratlan
Ahogy látható, a ‘90-es és ‘70-es évek eredményei között már nincs átfedés, ugyanígy a korábbi évtizedek között sem lesz a századfordulók kivételével, mivel az egyes évtizedekre az eredmény intervallumok hossza 18 év, és 22 év az intervallumok kezdőpontjai közötti különbség.Átfedés tehát 199x-201x és 198x-200x között van. Egészen pontosan 1992-2010, 1993-2011, …, 1999-2017 és 1982-2000, 1983-2001, …, 1989-2007 a lehetséges születési évszám párok ahol a művelet elvégzése után ugyanazt a számot kapjuk. Bár a kérdés szövegezése nem egyértelmű (“csak akkor teljesülhetne” - lehetséges hogy Zsolti is másik évben szülessen, vagy feltételezve hogy Zsolti ugyanabban az évben születik mint a valóságban), de a legkésőbbi az 1999-2017 pár, így valószínű hogy a 2025-2017=8 a várt válasz.
-

jerry311
nagyúr
Nem tudom ez mi volt, nem a saját gyerekem, csak így megkaptuk, baráti körben, hogy ezzel (is) jött haza a gyerek az első matek óráról most 5.-ben.
Excellel megvolt a brute force, amikor a hsz-t írtam. Csak gondoltam létezik esetleg valami elegánsabb megoldás mint számolgatni.
Ezek a párok, ahol egyeznek az összegek:
1982 2000
1983 2001
1984 2002
1985 2003
1986 2004
1987 2005
1992 2010
1988 2006
1993 2011
1989 2007
1994 2012
1995 2013
1996 2014
1997 2015
1998 2016
1999 2017És az utolsó feltétel miatt (=ha Zsuzsi későbbi évben született volna...) csak 1999 lehet a helyes.
Így Zsolti életkora 8.Mondjuk, nyilván ez egyéni szociális probléma, de a "néhány év korkülönbség" nálam 10 alatti, nem pedig 18. Ez egy ilyen upsz, becsúszott egy kistesó, vagy apa szerzett egy fiatalabb feleséget és lett egy féltestvér.
Ha kevésbé értelmezem a jelenben, akkor lehetne 1899 és 1908, Zsolti pedig 117 éves.
-

axioma
Topikgazda
válasz
 jerry311
#6673
üzenetére
jerry311
#6673
üzenetére
aranymedve[+] szint az azert ha sajat korosztalyos, az inkabb szorgalmi...
gyanitom 1999-es lesz, mert ott lesz egy drasztikus csokkenes az osszegnel, de most lusta vagyok bizonygatni
[igazabol az utolso 100 evre kepezed az osszes osszeget, es megnezed melyik a legutolso ami mondjuk az elozo 10 ev osszegei kozott mar szerepel - raadasul amikor nincs tizesatlepes, akkor no, szoval nem kell mindet szo szerint osszeadogatni] -

jerry311
nagyúr
Ez elméletileg 5. osztályos tananyag. Valaki esetleg felvilágosítana, hogy egyáltalán merre kellene elindulni?
-

VoidXs
nagyúr
Wow, ez a komment de rég volt. A választ 3 éve keresem, végre megtaláltam, és ordenáré hülyének érzem magam, hogy ezt egy jó Google keresés megtalálta volna... A DCT 4. verzióját írtam le, csak a dokumentum, ahonnan szedtem a képletet, ezt elfelejtette közölni, csak az algoritmust írta le...
-

VoidXs
nagyúr
Mielőtt megmutatom a megoldást, szeretném hangsúlyozni, hogy ezek a feladatok soha nem gyakorlatiak, a brute force (rajzolgatás, hátha kijön) sosem ér maximum pontot, csak indirekt bizonyítási esetekben.
Ha N darab egyenesed van, amik definíció szerint végtelen hosszúak, és egyik se párhuzamos semelyik másikkal, minden esetben minden egyenesen N - 1 metszéspontod lesz. Ez azért van így, mert valahol bármelyik kettő garantáltan metszeni fogja egymást, hiszen nem párhuzamosak. 4 esetén mind a 3 másikkal lesz egy metszésed. Mivel egy egyenesen N - 1 metszés van, ezért a majdnem végleges megoldás N * (N - 1), de ezt meg kell felezni, hiszen mindkét metsző egyenes szemszögéből leszámoltuk.
A végső megoldás tehát azt mondja, hogy N darab, páronként nem párhuzamos egyenes esetén pontosan N * (N - 1) / 2 metszéspont lesz, ami 4 egyenesnél 4 * 3 / 2 = 6 metszés. 5 nem fordulhat elő, az azt jelenti, hogy csak nem húztad elég hosszan az egyeneseket. Ha elég hosszan húzod, bárhogyan rajzolod fel őket, fixen 6 lesz:
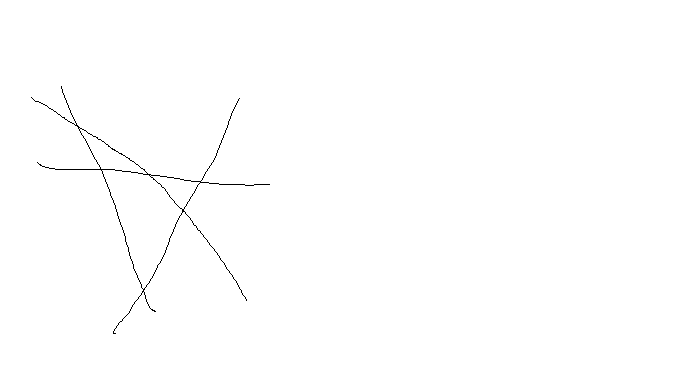
És ez az, ami miatt a rajzolás nem elégséges válasz, mert szinte mindig ki fog jönni próbálgatással, csak azt nem tudjuk, hogy miért.
-

coco2
őstag
Sziasztok!
Matematika feladatlap 6. évfolyamosok számára (ált. iskola) 2021 jan 28-as dátummal (interneten találtam) egy feladatban (9.a pont) gyakorlatilag azt kérdezi, mennyi a legtöbb metszéspont, amit 4 darab egymást nem fedő egyenessel létrehozni tudok?
Én találtam módot 5-re. A megoldás azt mondja, 6. Hogyan van az?
-

hiperFizikus
senior tag
Hardy-Ramanujan szám: Az 1729-es számot Hardy-Ramanujan számnak nevezik, mert ez a legkisebb pozitív egész szám, amely kétféleképpen is kifejezhető két köb összegeként:
1729 = 1³ + 12³ = 9³ + 10³

-

VoidXs
nagyúr
válasz
 hiperFizikus
#6659
üzenetére
hiperFizikus
#6659
üzenetére
Prímszámokról beszélünk, tehát triviális, hogy 0 megoldásuk lesz:
- Szorzás: két szorzat akkor egyenlő, ha a prímtényezős felbontásuk azonos. Ha mindkét oldal más prímekből áll, nem lehet azonos.
- Osztás: a/b=b/c esetben azt kellene bizonyítanod, hogy b=n*a és c=n*b, vagyis nem lennének prímek.
- Hatvány: mint a szorzásnál, prímtényezős felbontásokat készítesz, amik a kitételeid miatt soha nem lehetnek egyenlők. -

VoidXs
nagyúr
válasz
 hiperFizikus
#6657
üzenetére
hiperFizikus
#6657
üzenetére
Ez meg megint a Goldbach-sejtés. Ha megoldod, rögtön hozzád fognak vágni 1 millió dollárt, viccen kívül.
-

VoidXs
nagyúr
válasz
 hiperFizikus
#6654
üzenetére
hiperFizikus
#6654
üzenetére
Nem tudsz vele tovább jutni:
- ha x 3-as maradéka 0, akkor x osztható 3-mal,
- ha x 3-as maradéka 1, akkor x+2 osztható 3-mal,
- ha x 3-as maradéka 2, akkor x+4 osztható 3-mal.#6655 egyenletrendszere pedig, ha jól értem: a + b = b + c, és a, b, c prímek. Ekkor csak egy megoldás létezhet, a triviális, hiszen ha b kiesik, akkor a = c marad, és b a kiesés által szabad változóvá válik. Ha kikötöd, hogy a < b < c, akkor a megoldás üres halmaz, hiszen ha a = c, akkor b nem lehet az egyiknél kisebb, a másiknál pedig nagyobb.
-

hiperFizikus
senior tag
válasz
 hiperFizikus
#6654
üzenetére
hiperFizikus
#6654
üzenetére
Sőt komplikálhatjuk úgy is, hogy nem csak a két különbségnek kell egyenlőnek lennie, hanem foglalkozunk avval is amikor a két összege egyenlő !
Izgalmas, hogy van-e olyan négyes, ami négyesnek a egyenlő a különbsége is és egyenlő az összege is ! Persze az abszolút értékük egyezése nem valószínű !

-

VoidXs
nagyúr
válasz
 hiperFizikus
#6652
üzenetére
hiperFizikus
#6652
üzenetére
2-vel csak a 3, 5, 7 működik, nincs más, a fent említett okokból.
-

hiperFizikus
senior tag
persze lehet egyszerűsíteni 3 db-ra, de ekkor az értelemszerűen vett két különbségnek egyeznie kell !

azért kell több mert valami különlegeset szeretnék velük előállítani
"prog szempontbol az optimalizacio talan meg egy relevans kerdes"
Nem tudom, még sosem csináltam, teljesen új .

-

axioma
Topikgazda
válasz
 hiperFizikus
#6645
üzenetére
hiperFizikus
#6645
üzenetére
nincs ertelme a szamparokat tobbszor mas sorrendben felsorolni, ezert az a<b<c egy jo kikotes es [a,b],[b,c] a szamparok parja
igy az is latszik hogy a ket kulonbseges felteteled ugyanaz [amugy kulonbozo a,b,c,d-re is tok trivialisan]
mire kell neked tobb, es tobb vagy nagyobb? iratsz chatgpt-vel egy programot ra es futtatod orrverzesig... ebben semmi matek azon tul, hogy egyszerusitettuk a feltetelrendszert
prog szempontbol az optimalizacio talan meg egy relevans kerdes: alulrol haladsz es a,b-bol krealt c-t ellenorzod vagy uj c primre nezed hogy van-e a,b [nyilvan alulrol a 3-mal osztas miatt csak a 3,b,c es az a,b ugyanolyan maradekot ad 3-ra esetek erdekesek, egyszerubb kulon halmazban nyilvantartani mint ellenorizni] - de az se ide valo mar -

VoidXs
nagyúr
válasz
 hiperFizikus
#6645
üzenetére
hiperFizikus
#6645
üzenetére
Magyarul olyan a - b = b - c esetet keresel, ahol a, b, c prím, erre rengeteg példa van a tiéden kívül, pl. 3 - 7 = 7 - 11, vagy 5 - 11 = 11 - 17. Valószínűsíthető, hogy végtelen ilyen számhármas létezik, de jelenleg a matematika egy meg nem oldott problémája, hogy milyen szabályrendszer van prímek távolsága közt (a Goldbach-sejtést kellene hozzá megoldani). Programmal könnyen találsz rengeteg ilyet, de egy idő után már nagyon lassan dobál ki új számokat.
-

axioma
Topikgazda
válasz
 hiperFizikus
#6643
üzenetére
hiperFizikus
#6643
üzenetére
Nem ertelek. Ket primpar kell, legalabbis a korabbibol ez jott ki. Mar ha a par azt ugy erted, ahogy szoktuk, hogy 2 kulonbseguek. Amik vannak vegtelenul, ugyhoyg a parok parjai is.
p1,p1+2 es p2,p2+2
ekkor a parokon belul nyilvan 2 a kulonbseg, hiszen olyanokat keresel
a p2-p1 pont annyi lesz, mint (p2+2)-(p1+2).
De mi az az 5 vagy 5 faktorialis?Vagy azt erted, hogy p1, p2, p3 primszamok parokba rendezve (p1,p2) es (p2,p3) ahol p2-p1 = p3-p2? A 3-mal oszthatosag ott is fennall, tehat p1=3 kell, es p2 prim ahol 2*p2-3 is prim. Ez a cel?
-

hiperFizikus
senior tag
Amikor az egyik pár belső különbsége és a másik pár belső különbsége egyenlőek egymással, akkor ... !
A ('3', "5") | ('5', "7") a legkisebb ilyen pár_pár, ezért egy kis asszociációs zavart okoz, de a magasabb ilyeneknél talán már nem lesz ilyen asszociós zavar !
Találtam is egy érdekességet:
1. ('3', "5") | ('5', "7") => 2 : "7"-"5" = '5'-'3' : másmilyen külső különbségek egyenlősége állnak fenn
2. és (3, "5") | ("5", 7) => 5 ! : {3, 5, 5, 7} -> {3, 5, 7} : ugyanolyan tartalmak állnak fenn
-

axioma
Topikgazda
válasz
 hiperFizikus
#6641
üzenetére
hiperFizikus
#6641
üzenetére
azt meg ertem hogy primparokat keresel, de mi az az 'ilyesmi'? nem tul standard a jelolesrendszered...
nyilvan tobb olyan nincs h p, p-2 es p+2 is prim, az egyik tuti oszthato 3-mal, igy az maga a 3
-

hiperFizikus
senior tag
Ez biztosan nem off :
Találtam is egy érdekességet:
1. ('3', "5") | ('5', "7") => 2 : "7"-"5" = '5'-'3'
2. és (3, "5") | ("5", 7) => 5 ! : {3, 5, 5, 7} -> {3, 5, 7}Keresetek nekem ilyesmi szorosan értelmezett (törzszám?) párokat !
E szám pároknak nem kell közvetlenül egymást követő törzsszám-pároknak lenniük !
-

lajafix
addikt
válasz
 husztiimi
#6637
üzenetére
husztiimi
#6637
üzenetére
Hány pont kell a kinézett iskolához? A feladatsor jó, de még jobb ha irányított a felkészülés, nálunk egy online matek kurzus jobban bejött a kisebbnél, mint a nagyobbnàl az akkor kinézett iskola általi matek felkészítő, egyszerűen jóval lelkesebbek voltak az online tanárok. Pontokban: 26 vs 45 az ötvenből.
-

axioma
Topikgazda
válasz
 husztiimi
#6637
üzenetére
husztiimi
#6637
üzenetére
A te kerdesed az ami pont idevalo... a tobbi velemenyes.
Az irasbelire a legjobb, ha vegigcsinalja az elmult evek feladatlapjait. Van megoldokulcs, es szerintem ha abbol se egyertelmu, azzal mehet a tanarhoz, de aka'r ide is. Evente van potalkalom feladatsor is, szamoljatok ki, es a multbol induljatok, a frisset csinalja utoljara. A legjobb, ha eleve ugy idore es egymas utan[!] csinalja a magyar/matek feladatsorokat, ahogy ott lesz [jellemzoen hetvegen fer jol bele].
Azt is olvassa/olvassatok el a megoldokulcsbol, amire semmit nem irt. -

husztiimi
csendes tag
Ha kérdésem nem ebbe a topikba való, akkor bocsi...
Az egyik gyerekem a sok közül jövőre lesz nyolcadikos. Milyen matematikai tankönyv javallt a felkészülésre a felvételire? -Nem lenne baj, ha nemcsak a feladatok lennének a könyvben, hanem a megoldások/megoldókulcs is.
-

hiperFizikus
senior tag
válasz
 hiperFizikus
#6635
üzenetére
hiperFizikus
#6635
üzenetére
Kitaláltam egy új halmazelméletet, természetesen a hozzá tartozó axióma rendszerrel együtt ! A ChatGPT MI sokat segített érte !

-

hiperFizikus
senior tag
válasz
 hiperFizikus
#6634
üzenetére
hiperFizikus
#6634
üzenetére
#549
Ezen felbuzdulva megpróbáltam alkalmazni (⎖ ⍻ ∦) őket a pszichére is magyarul a lélekre ! A ChatGPT MI segítségével ez egészen jól is sikerült !
-

hiperFizikus
senior tag
válasz
 hiperFizikus
#6628
üzenetére
hiperFizikus
#6628
üzenetére
Kitaláltam valami matekos új operátort ! Segítségével a különféle analitikus képletek közt teremthetünk képzelet beli kapcsolatot !
#47
Az új kvázi-logaritmusom az egyesítő fizikákért !
Az ad hoc tudományok polcáról !

szürkébe tettem -

Tsoi
csendes tag
Sziasztok,
segítsetek légyszi az alábbi feladatban:
adott egy 260mm átmérőjű hengeres test, ami alá van támasztva 3 ponton (36fok,179fok,260fok) és 240mm átmérőn. Mérjük a henger alapját (magasságát) 3 ponton:
Pont 1. 0 fok
Pont 2. 93 fok
Pont 3. 228 fokHogyan tudom meghatározni a mért érékek alapján, hogy a henger pontosan merre dől (0-360 fokban) és mekkora az alátámasztás értéke (mm)?
Előre is köszi!

-
-

HellGreg
őstag
Sziasztok! Hogy kell osztásos egyismeretlenes egyenletet kiszámolni (hatodik osztályos)?
pl:
5/8 : X = 3/14
Azt tudom, hogy a törtek osztásánál az osztó reciprokával kell szorozni, de ennél a példánál elakadtunk, mert hiába képzelek bármilyen számot X helyére, nem jön ki sehogy 3/14.
Szóval feltételezem van valami menete ennek, ahogy hivatalosan ki kell számolni, a tankönyvben viszont csak az alap van megmagyarázva, tehát hogy osztásnál az osztót reciprokra kell alakitani, és 2 feladat után már ilyenek jönnek. Józan paraszti ésszel próbáltam 5/8-ot szorozni 3/14-del, de úgy se jött ki. -

hiperFizikus
senior tag
válasz
 hiperFizikus
#6612
üzenetére
hiperFizikus
#6612
üzenetére
#18
A kőkorszaki 2!5. kettes számrendszer !
Logaritmus számítás a kőkorszakban ?Bebizonyítottam, hogy a kőkorszakban a kettes számrendszert használták ! Ha elolvassátok e rövidke tanulmányomat, akkor ti is be fogjátok látni, hogy igazam van !
A 100 ezer évvel ezelőtti logaritmus számolásra meg alapos gyanúm van !
szürkébe tettem -

VoidXs
nagyúr
válasz
 hiperFizikus
#6625
üzenetére
hiperFizikus
#6625
üzenetére
Ha már rögtönzött filozófia topikot tartunk senki élvezetére, olvasd el inkább újra, emészd egy kicsit.
-

hiperFizikus
senior tag
Ez csúnya és nem is okos ! Ha az agyadat akarod használni, akkor minimum követelmény, hogy a kémiai felesleges élvezeti cikkek függőségétől mentesíted az agyad ! Ha már rá vagy szokva, akkor nehezebb lehet, de az is okos dolog, ha befekszel elvonókúrára ! - igazán okos dolog lenne .

-

VoidXs
nagyúr
válasz
 hiperFizikus
#6623
üzenetére
hiperFizikus
#6623
üzenetére
Nem vagyok matematikus, de egy értelmiségi előtt két út van, az egyik az alkoholizmus, a másik járhatatlan. Szóval általában szarul.
-

VoidXs
nagyúr
válasz
 hiperFizikus
#6621
üzenetére
hiperFizikus
#6621
üzenetére
Mire jutok mivel?
-

VoidXs
nagyúr
válasz
 hiperFizikus
#6619
üzenetére
hiperFizikus
#6619
üzenetére
Embeddált bizonyítás nélkül nem értem, hogy mi itt a nagy újdonság. Ha itt arra gondolnak, hogy C = 90° esetén a szinusztételből
a = c * sin(A),
és
b = c * sin(B) = c * cos(A),
mert A + B = 90°, akkor behelyettesíted Pitagoraszba, és kijön, hogy c^2 = c^2. Ezt tényleg össze lehet rakni középiskolában, max azt tudom elképzelni, hogy igény hiányában nem írta le senki, bár az is fura.Szerk: megnéztem, és persze, hogy erősen hibás volt a cikk, rengeteg előkövetelményt lehagyott, ezért nem olvasunk tech/tudomány cikkeket olyan oldalon, aminek nem ez a profilja.
-

hiperFizikus
senior tag
https://hvg.hu/tudomany/20241029_pitagorasz-tetel-bizonyitasa-trigonometria-korkoros-erveles
"A matematikusok sokáig úgy gondolták, hogy trigonometriával nem lehet a Pitagorasz-tételt bizonyítani, mert az érvelési hibához vezet. Két fiatal amerikai diáklány azonban bebizonyította, hogy ez nem így van."Vagyis a diplomás matekusk is lehetnek h..lyék ! - hát ilyesmit azért nem vártam .

-

VoidXs
nagyúr
válasz
 hiperFizikus
#6616
üzenetére
hiperFizikus
#6616
üzenetére
Tudunk hatványozni és gyököt vonni, ennél azért jelentősen komplexebb problémaköröket szoktunk itt fejtegetni.
-

hiperFizikus
senior tag
de hát ez egy matematika topik
én a hatványozásról és a gyökvonásról írtam
és az benne a feladat, probléma, hogy egy eddig feltáratlan formalizmus alapján hatványoztak és gyököt vontak
ha úgy gondoljátok, hogy a sok ezer évvel ezelőtt nem érdekes, akkor gondolhattok rá mint valami új formális nyelvre

-

TDX
tag
válasz
 hiperFizikus
#6614
üzenetére
hiperFizikus
#6614
üzenetére
Szerintem nem érdekes az embereknek ebben a topicban, azért nem szól hozzá a hozzászólásaidhoz senki.
-

axioma
Topikgazda
válasz
 hiperFizikus
#6612
üzenetére
hiperFizikus
#6612
üzenetére
nem azt mondtam h semmi koze a matekhoz, hanem hogy nem erdekes a topik szamara
de ott a lehetoseg, modiknal jelezheted hogy nem ertesz egyet -

axioma
Topikgazda
Toroltem, mert tobbszori keres ellenere uralod a temat, a kozony ellenere. Keresd meg legyszi a kozonsegedet, ne ide 'szemetelj'!
-

hiperFizikus
senior tag
válasz
 hiperFizikus
#6604
üzenetére
hiperFizikus
#6604
üzenetére
https://erdosattilask01.lapunk.hu/helyerteku-szamolas-a-kokorban-1214376
Helyértékű számolás a kőkorban !Ellenőrizétek már, hogy nem tévesztettem-e el valamit !

-

axioma
Topikgazda
válasz
 hiperFizikus
#6607
üzenetére
hiperFizikus
#6607
üzenetére
A tortenelmi resz semennyire, de nem en szamitok, hanem az atlagolvaso.
Irj inkabb blog-ot (itt logout-on belul is tudsz), aztan ha parhavonta egyszer bekuldesz ide egy linket egy uj irasra az me'g belefer. -

axioma
Topikgazda
válasz
 hiperFizikus
#6605
üzenetére
hiperFizikus
#6605
üzenetére
Mar jeleztem, hogy ne spammeld a topikot!
-

hiperFizikus
senior tag
válasz
 hiperFizikus
#6604
üzenetére
hiperFizikus
#6604
üzenetére
8.+
Nagyon úgy néz ki, hogy ezek a bogárjeleik a 0 jelünk megfelelője, csak ők - a kőkorszakiak - megint csak másképpen használták mint mi ! Náluk a más-más alakú bogárjelek más-más 0 jel csoportosítást jelöltek:pl. az egyik bogárjelük az ezresét, a másik bogárjelük a millióét, a harmadik bogárjelük a milliárdot jelölte !

-

hiperFizikus
senior tag
válasz
 hiperFizikus
#6603
üzenetére
hiperFizikus
#6603
üzenetére
https://erdosattilask01.lapunk.hu/a-kokorszaki-szamabrazolas-logikaja-1214371
A kőkorszaki számábrázolás logikája !
"Tehát a kőkorszaki táblákon valamennyi számábrázolást alkalmazták ! Sajnos ennyi önmagában nem elég a kőkorszaki leletek általános megfejtéséhez, de e nélkül szinte lehetetlen megfejteni őket !Az, hogy egyáltalán van értelme a megfejtésükkel foglalkozni, csak az teszi lehetővé, hogy a rövid rézkorszak földrengés szerű törést hozott a bronzkorszakba való átmenetkor ♥ "
-

hiperFizikus
senior tag
válasz
 hiperFizikus
#6602
üzenetére
hiperFizikus
#6602
üzenetére
https://erdosattilask01.lapunk.hu/a-kesoi-neolitikum-korszak-irasa-es-matematikaja-1214353
A késői Neolitikum kőkorszak írása és matematikája !Sikerült megfejtenem, nem hagyhatjátok ki !

Ez meg a minószi lineáris A írás számábrázolása lenne a késői Neolitikum kőkorszakból : Jól látható, hogy egyszerre vízszintes is és függőleges is és főleg derékszögűek is ! - legalábbis jobban közelítenek a derékszöghöz, mint a Húsvétszigeti ilyenek .
Ezek a kereszteződő pálcika alakú ikongramok számokat is és szavakat is jelöltek egyszerre, mint egy katalógus .
A balra lévő első keresztes pálcák ikon szavakat jelölnek, a sorában utána következő ikongarmok meg már rendesen számokat és műveleteket jelölnek ! Majd a magyarázatomból ki fog derülni, hogy - hihetetlen, de - ismerték az összeadást is, a kivonást is, a proto-szorzást is és a proto-osztást is, hogy még mit az majd ki fog derülni a következő magyarázatomból ! - azoknak akik nem szeretik a matematikát: erősen nem ajánlott tovább olvasniuk: érted "allergiás rohamot" kaphatnak tőle .
Igazán érdekes, és a mi modern matematikánktól teljesen eltérő, de működő matematika: kattints érte a linkemre !igazán kíváncsi vagyok a véleményetekre róla


-

hiperFizikus
senior tag
Tudom, hogy harugusztok rám, de a segítségeteket kell kérnem, mert nem bírok evvel az algebra-számtani feladvánnyal ? - előre is köszönöm, hogy nem moderáltok ki.
https://erdosattilask01.lapunk.hu/a-minszi-linearis-a-iras-megfejtese-1214352
A minószi lineáris A írás megfejtése !" Ezen a lelet felvételén a minósziak matematikája látható: lineáris A írással !
https://hu.wikipedia.org/wiki/ ... .jpgTalán nincs is még egy ilyen lelet a szériában, ezért borzasztóan fontos ami rajta van ! Uyanis a Rongo-rongo írások közt is van egy napló, ami a Rongo-rongo írás matematikáját tartalmazza ! Kiderül belőle, hogy a Rongo-rongo írás zárójelezést használ, tőlünk eltérő zárójelezést ! => írtam is rá egy a minktől eltérő algebrát ♥
Esetleg ebből a matekos leletből is egy még újabb algebra teremtődhet: ezért lenne fontos borzasztóan az, ami rajta van !
Íme, lássa hát mindenki /: Akárhogyan is nézem, én még nem tudtam eligazodni a matekján, hátha neked sikerül ♥
Viszont ugye szerintetek is túlságosan hasonlít a kínai ideogramákra ? "Ha megpróbálnád ezt az algebrát megfejteni, akkor kattints a linkemre érte ♥

Új hozzászólás Aktív témák
- Milyen egeret válasszak?
- Autós topik
- Két generációval korábbi GeForce gyártása indulhat újra
- Warhammer 40.000
- Nvidia GPU-k jövője - amit tudni vélünk
- GL.iNet Flint 2 (GL-MT6000) router
- One otthoni szolgáltatások (TV, internet, telefon)
- Visszatérnek a Samsung tervezte CPU-magok és GPU az Exynos 2800-ban?
- 5.1, 7.1 és gamer fejhallgatók
- QWERTY billentyűzetes, üzenet-fókuszú androidos mobil a Clicks Communicator
- További aktív témák...
- 184 - Lenovo Legion Pro 7 (16IAX10H) - Intel Core U9 275HX, RTX 5090 (ELKELT)
- Apple iPhone 13 ProMax 256GB Kártyafüggetlen 1év Garanciával
- Ezviz BC1 1 kamerás kamera szett / 12 hó jótállás
- Xbox One S 1 TB + kontroller 6 hó garancia, számlával!
- HIBÁTLAN iPhone 13 Pro 256GB Sierra Blue -1 ÉV GARANCIA - Kártyafüggetlen, MS3022
Állásajánlatok
Cég: PCMENTOR SZERVIZ KFT.
Város: Budapest
Cég: Laptopszaki Kft.
Város: Budapest















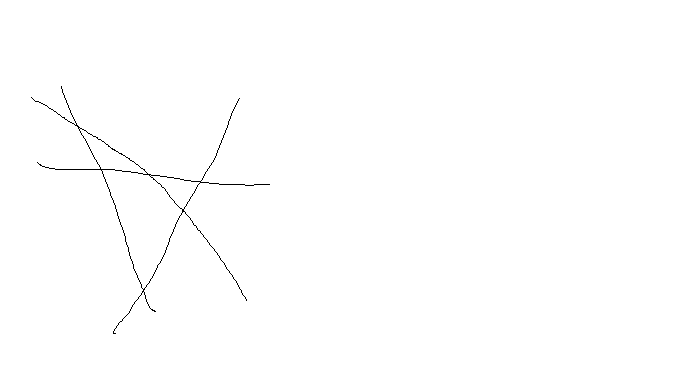












![;]](http://cdn.rios.hu/dl/s/v1.gif)